#동역학

감쇠의 종류
(1)마찰감쇠 : 접촉면과의 마찰
(2)점성감쇠 : - 공기저항 (유체의 점성에 의한 감쇠)
- 분자와 분자 사이의 마찰 (물질의 점성에 의한 감쇠)
(3)이력감쇠 : 비탄성영역에서 하중반전 시 일어나는 에너지 소산에 의한 감쇠
구조물이 감쇠: 탄성해석시 5% [(1)+(2)+(3)]
비탄성 해석 시 2.5% [(1)+(2)]
비탄성 해석 시 비탄성영역 이력 거동 직접 반영
운동방정식 = 관성력+감쇠력+탄성력 ( m·x'' + C·x' + k·x =0 )
관성력 : 운동상태를 유지하려고 하는 힘

감쇠력 : 운동상태를 감소시키려고 하는 힘

탄성력 : 변형에 저항하여 원래대로 돌아가려고 하는 힘

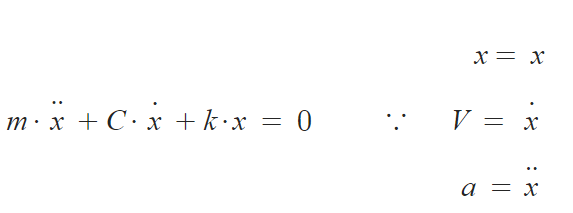
단위 :
- 질량(m)
m=P/g = 무게(kN) / 가속도(9.81m/s^2) = kN · sec^2 / m = ton
- 감쇠상수(C)
C = kN · sec / m
- 강성(k)
k = kN/m
구조물의 강성 (k)




감쇠가 없을 때 고유각진동수 (w)
운동방정식에 의해

deSolve(x''+w2*x=0, t, x)
a*cos(w*t) +b*sin(w*t)→ x
경계조건 : 초기변위 x(0) = xo :
solve((x|t=0)=xo, a) → a
초기속도x'(0)=Vo :
solve((d/dt(x)|t=0)=Vo, b) → b
비감쇠 일때의 해

감쇠 자유진동
구조물의 이상화, 자유물체도

특성방정식

해가 3가지가 있을 수 있음
(1) 1개의 근이 있을 경우 : s1 = s2 → 임계감쇠 (C^2-4*k*m=0) 근이 하나
(2) 2개의 근이 있을 경우 : s1, s2 → 과감쇠 (C^2-4*k*m>0) 실수
(3) 2개의 허근이 있을 경우 : → 저감쇠(진동) (C^2-4*k*m<0) 허수
감쇠가 있을 때 고유각진동수 (wd)
특성 방정식 : m · s2+C · s + k = 0
C = 감쇠상수 ( kN·sec / m )
Ccr = 임계감쇠상수 ( kN·sec / m )
임계감쇠
Ccr2 - 4 · k · m = 0

과감쇠
Ccr2 - 4 · k · m > 0

저감쇠 (일반적으로 구조물의 감쇠율은 10%미만이므로 저감쇠에 해당된다)
Ccr2 - 4 · k · m < 0

건축구조물은 대부분 저감쇠이다.
저감쇠일 때 의 해

ξ = 감쇠율
고유진동수 (f)
f = 단위시간당 사이클 수 (cycle/sec = Hz) = w/2π
고유주기(T)
T = 1사이클에 걸리는 시간 (sec) = 1/f
단자유도 비감쇠 풀이방법
1. 단자유도
1-1. 자유진동(외력X)
1-1-1. 비감쇠
(1) 자유물체도 작성
(2) 구조물의 강성 k 산정
자유각 방향으로 하중 P를 준다 → 처짐 δ 를 구한다 → P = k · δ
- p*x → m1
+p*l - p*x → m2
m-p*x → m3 (m = 부정정차수)
∫ m(n)^2/(2*ei)dx → u
부정정 차수 있으면,
solve(d/dm(u)=0, m) → md/dp(u) → d
solve(p=k*d, k) → k = p/d = k

(3) 질량 m 산정
m = P/g ( kN·s2/m = ton) , where g = 9.81 m/s2
(4) 비감쇠 고유각진동수 w 산정

(5) 고유진동수 f , 고유주기 T 산정
f = w/2π (cycle/sec)
T = 1/f (sec)
예제)

단자유도 감쇠 풀이방법
1. 단자유도
1-1. 자유진동(외력X)
1-1-2. 감쇠
(1) 자유물체도 작성
(2) 구조물의 강성 k 산정
자유각 방향으로 하중 P를 준다 → 처짐 δ 를 구한다 → P = k · δ
- p*x → m1
+p*l - p*x → m2
m-p*x → m3 (m = 부정정차수)
∫ m(n)^2/(2*ei)dx → u
부정정 차수 있으면,solve(d/dm(u)=0, m) → m
d/dp(u) → d
solve(p=k*d, k) → k = p/d = k

(3) 질량 m 산정
m = P/g ( kN/m·s2 = ton) , where g = 9.81 m/s2
(4) 고유각진동수 wd 산정
deSolve(m*x''+C*x'+k*x=0, t, x)
↘ x = c1*nt*cos(wd*t)+C2*nt*sin(wd*t)
고유각진동수 wd = (rad/sec)
(5) 고유진동수 f , 고유주기 T 산정
고유진동수 f = wd / 2*π (cycle/sec)
고유주기 T = 1/f = 2*π / wd (sec)
(6) 감쇠율(ξ) 을 이용해서 T 산정 시
Ccr = √4·k·m (kN·sec/m)
ξ = C/Ccr
wd = w·√1-ξ2 (rad/sec)
T = 2*π/wd = (sec)
예제)
116회 - 2교시 - 1.
117회 - 4교시 - 1.
다자유도 비감쇠 풀이방법
2. 다자유도
2-1. 자유진동(외력X)
2-1-1. 비감쇠
이론 :

다자유도 비감쇠 풀이방법
2. 다자유도
2-1. 자유진동(외력X)
2-1-1. 비감쇠
(1) 자유물체도 작성
(2) 구조물의 강성 산정
자유각 방향으로 하중 Pn를 준다 → 처짐 δ 를 구한다 → P = k · δ
- p2*x → m1
-p2*l - p1*x → m2
∫ m(n)^2/(2*ei)dx → u
x1 = du/dp1 = f11*p1 + f12*p2
x2 = du/dp2 = f21*p1 + f22*p2
[u1, u2]T = [f] * [P] 매트리스 형식으로 산정
[f] → f
f-1→ k = [K]
(3) 운동방정식
[M]x[X''] + [K]x[X] = 0
(4) 고유치 해석을 이용해 고유각진동수 w 산정
고유치 해석에 의해 [X''] = -w2*[X]
([K]-w2x[M])x[X] = 0
[M] → mm
[K] → kk
solve(det(kk-w2*mm)=0, w2)
√w21 → w1
√w22 → w2 … (rad/sec)
(5) 고유진동수 f, 고유주기 T 산정
f1= w1 / (2*π) ,
f2= w2 / (2*π) , … (cycle/sec)
T1 = (2*π) / w1 ,
T2 = (2*π) / w2 , … (sec)
(6) 모드형상
kk - w12*mm →
solve(a1*u1+b1*u2, u2)
kk - w22*mm →
solve(a2*u1+b2*u2, u2)
예제)
113회 - 3교시 - 3.
104회 - 4교시 - 2.