3. 힘과 응력
1) 전단과 모멘트의 관계
2) 후크의 법칙 (Hook's Law)
3) 축응력 (Axial Stress)
4) 휨력 (Bending Stress)
5) 전단응력 (Shear Stress)
6) 전단중심
7) 합성응력
1) 전단과 모멘트의 관계
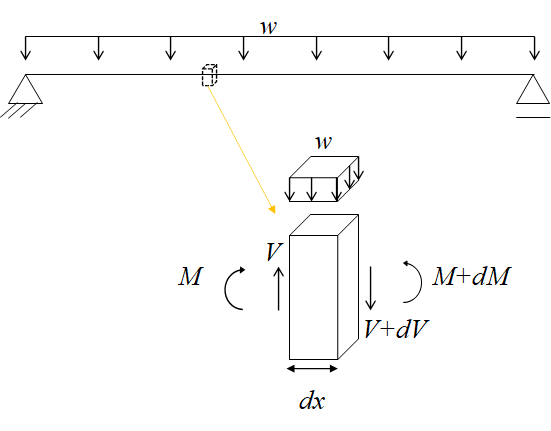
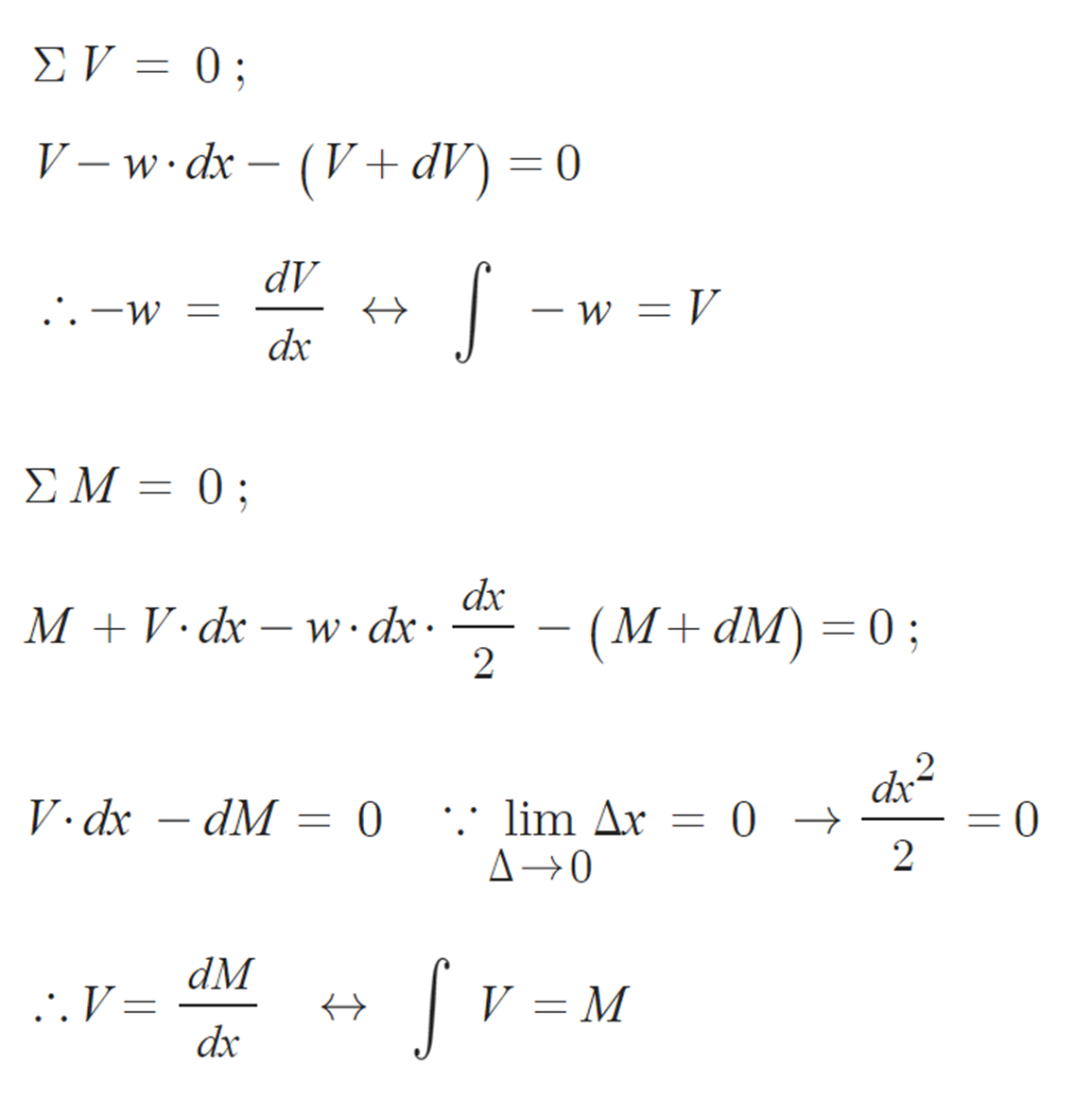
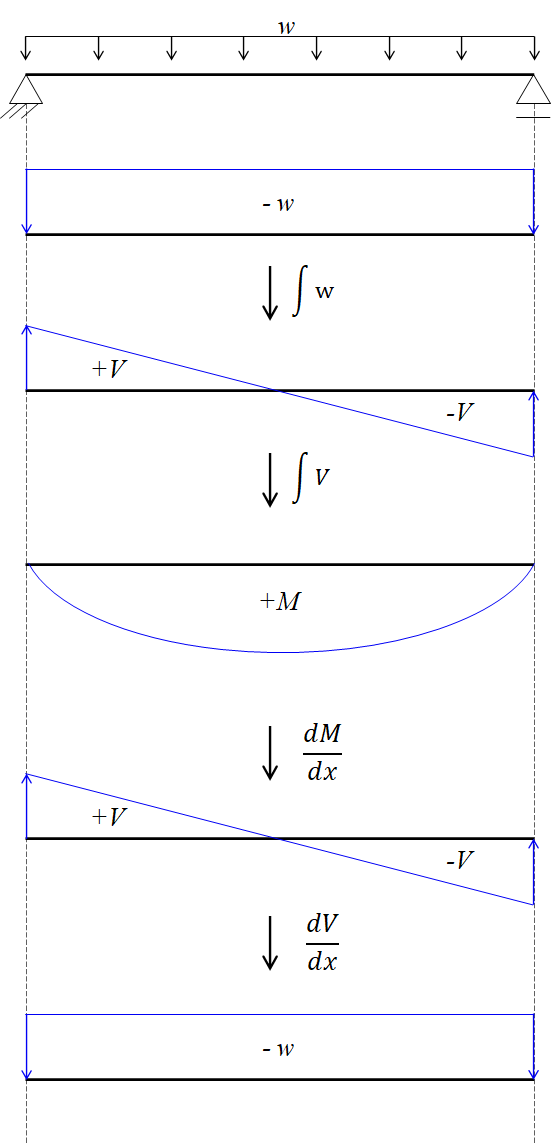
∴ 모멘트( M )을 미분하면 전단( V )이고, 전단( V )을 미분하면 하중( -w )이다.
= 하중( -w )을 적분하면 전단( V )이고, 전단( V )을 적분하면 모멘트( M )이다.
2) 훅 법칙 (Hook's Law) (출처 : 위키백과)
- 훅 법칙(영어: Hooke’s law)은 용수철과 같이 탄성이 있는 물체가 외력에 의해 늘어나거나 줄어드는 등 변형되었을 때 자신의 원래 모습으로 돌아오려고 저항하는 복원력의 크기와 변형의 정도의 관계를 나타내는 물리 법칙이다.
- 정의 : 매끈하고 평수마루 위에 용수철을 둔다. 용수철의 오른쪽 방향을 양의 x 축이라고 하자. 용수철 왼쪽 끝을 고정하고 외력이 없을 때 왼쪽 끝의 위치를 x 의 원점으로 잡자. 용수철 길이가 변했을 때, 오른쪽 끝의 x 좌표로 변형 상태를 나타내기로 한다. x > 0 이면 늘어난 것이고, x < 0 이면 줄어든 것이다. 용수철 길이의 변화가 x 일 때의 복원력을 F 로 하자. 힘이 오른쪽 방향이면 F > 0 이고, 왼쪽 방향이면 F < 0 이라 한다. 이 때, 훅 법칙은 다음과 같이 나타낼 수 있다.
F = - k·x
이 때 k 를 용수철 상수라고 부른다. 용수철 상수는 용수철의 힘 혹은 유연한 정도를 나타내는 상수로 각각의 용수철마다 다른 값을 갖는다.
3) 축응력 (Axial Stress)
① 축응력
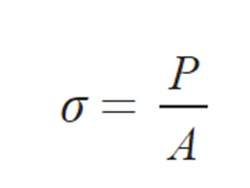
P = 축력 (Axial Froce)
A = 단면적 (Cross Sectional Area)
② δ : 축력에 의한 변위
그림 삽입 예정.
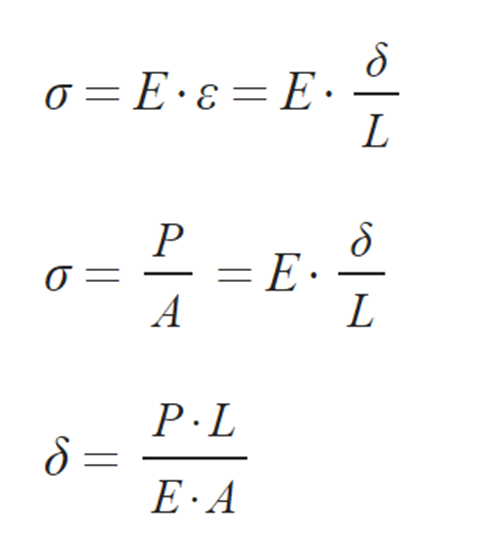
③ K : 강성도
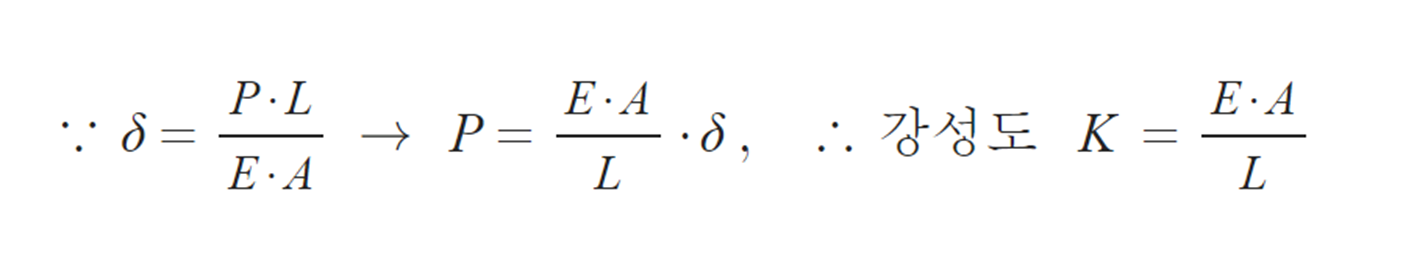
⑤ f : 유연도

⑥ δT 온도변화에 의한 팽창,수축
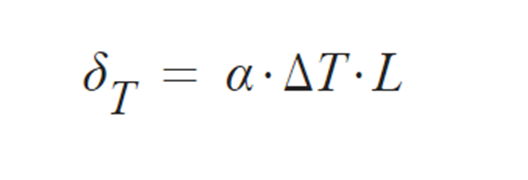
4) 휨력 (Bending Stress)
① 휨응력

M = 휨력 (Bending Moment)
y = (vertial distance away from the neutral axis)
② 유도과정 :
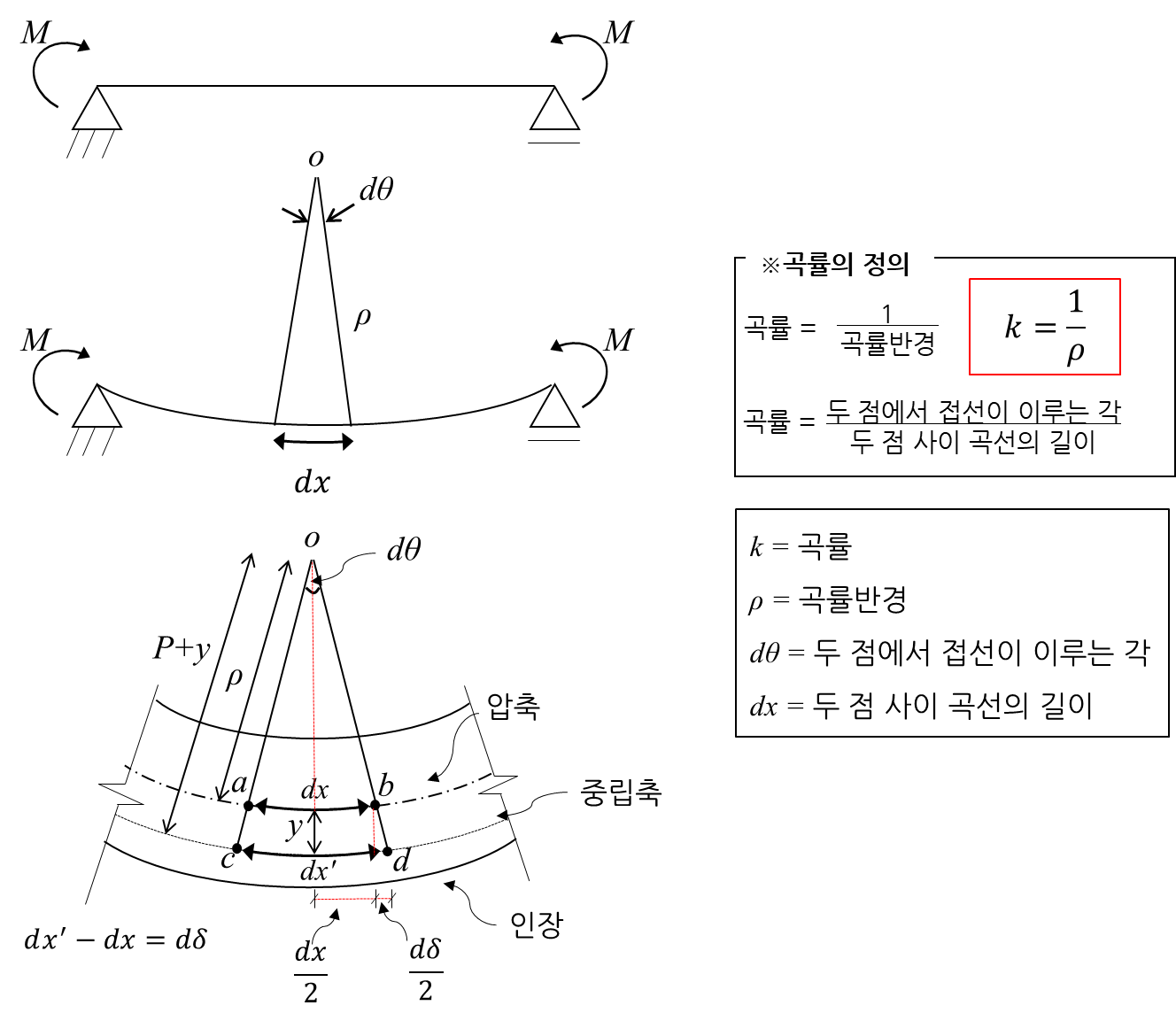

④ 변형률 ε_x 과 응력 σ_x 의 관계
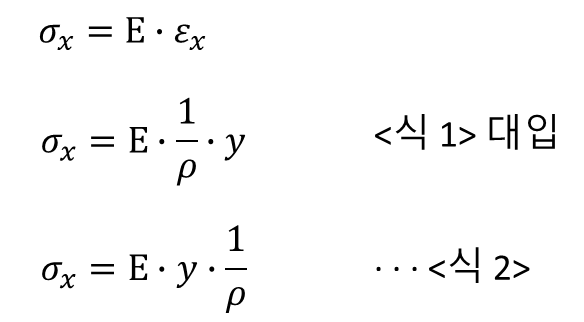
⑤ 모멘트 M 과 응력 σ_x 의 관계
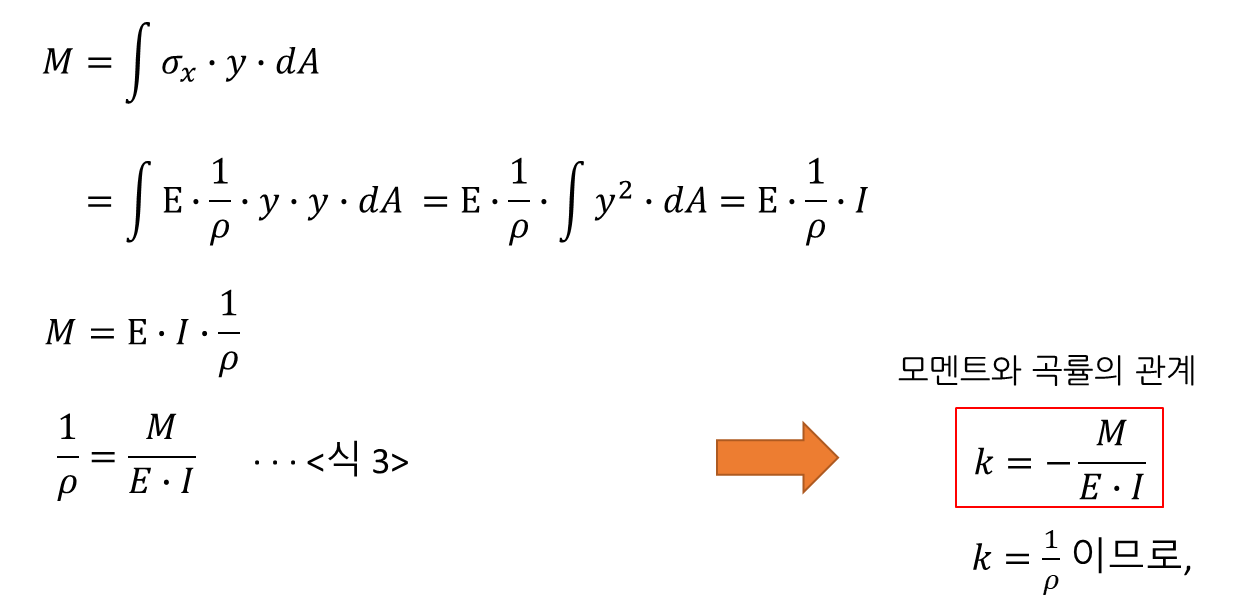
⑥ <식 2>에 <식 3>을 대입

⑦ 추가 : 탄성곡선 관계
탄성곡선 미분방정식 유도

5) 전단응력 (Shear Stress)
① 전단응력
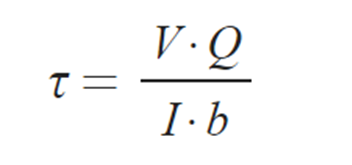
② 유도과정 :
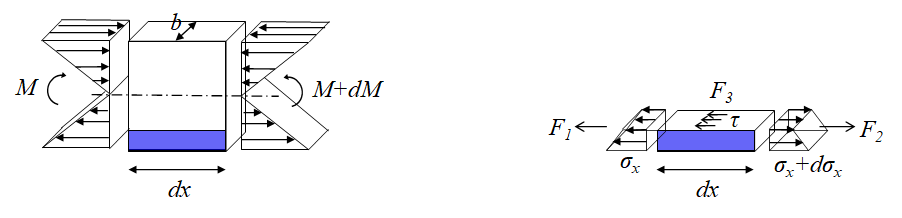
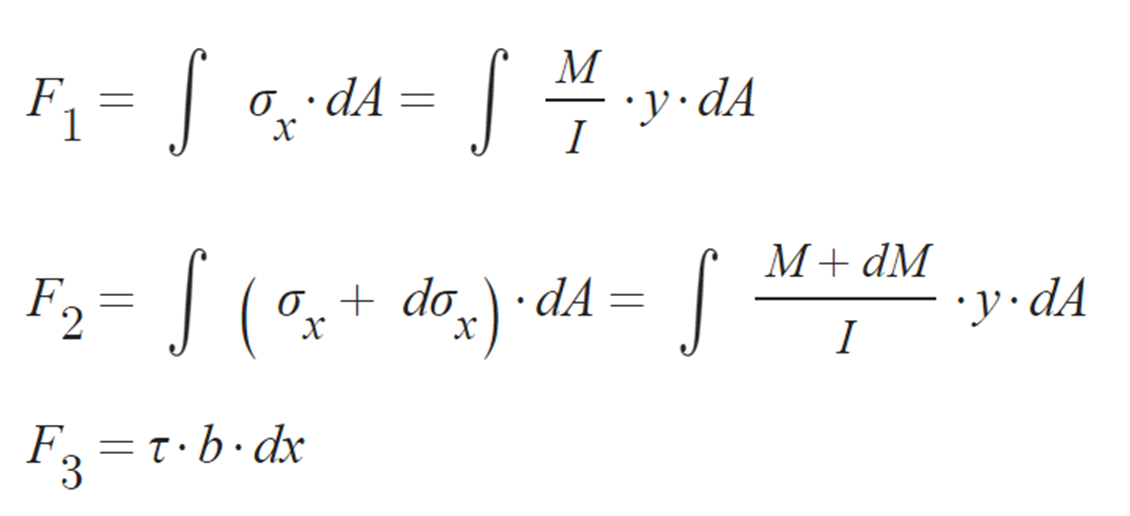
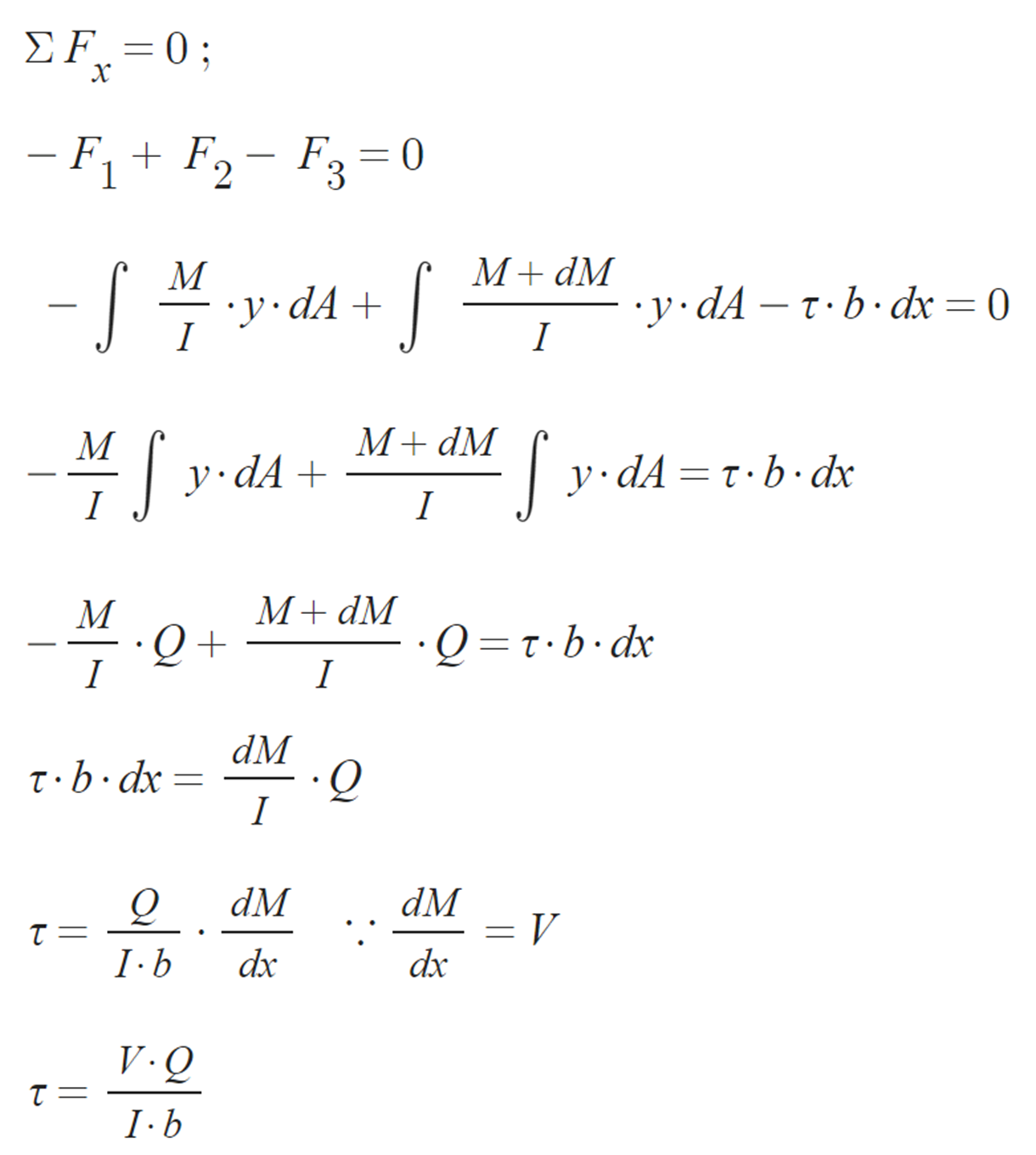
③ 전단흐름: 단위 길이당 전단력
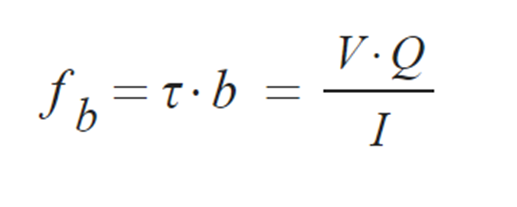
6) 전단중심 위치 산정 예제 :
전단중심 위치 산정 예제 :
7) 합성응력
'역학 > [1] 재료역학' 카테고리의 다른 글
| [2] 재료역학 5. 좌굴안정론 (Buckling) (0) | 2023.07.17 |
|---|---|
| [2] 재료역학 4. 주응력 주축 산정 (0) | 2023.07.10 |
| [2] 재료역학 2. 단면의 성질 (0) | 2023.06.30 |
| [2] 재료역학 1. 고유치 해석 (0) | 2023.06.30 |
| [2] 재료역학 (1) | 2022.04.06 |



