목차
1. 고유치 해석
2. 단면의 성질
1) 단면 1차 모멘트
2) 단면 2차 모멘트
3) 단면 상승 모멘트
4) 극관성 모멘트 (비틀림 상수)
5) 주축 주단면
(1) 모어원(Mohr's Circle)
(2) 고유치 해석
6) 탄성과 소성(중립축 & 계수)
7) 탄성계수(E)와 전단탄성계수(G)의 관계
8) 비틀림
3. 힘과 응력
1) 전단과 모멘트의 관계
2) 후크의 법칙 (Hook's Law)
3) 축응력 (Axial Stress)
4) 휨력 (Bending Stress)
5) 전단응력 (Shear Stress)
6) 전단중심
7) 합성응력
4. 주응력 주축 산정
1) 모어원(Mohr's Circle)
2) 고유치해석 (Eigen)
5. 좌굴 안정론
6. 탄성과 비탄성
- 세장비 개념
7. 주요 도형의 도심위치 와 면적
2. 단면의 성질
- 단위응력 '1'을 가진 단면의 특성을 각종 유용한 수치로 나타내어 재료의 물성치만 알면 곱해서 재료의 강도비를 산정함.
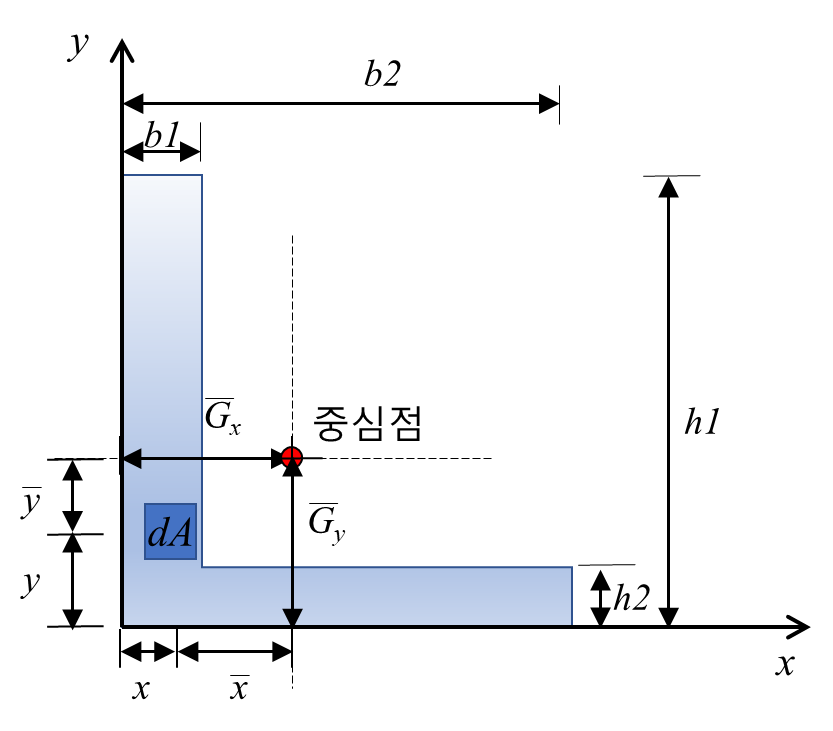
1) 단면 1차 모멘트
- 단면의 도심산정 시 사용
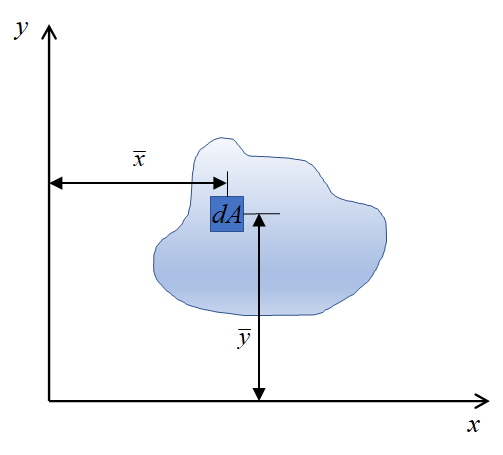
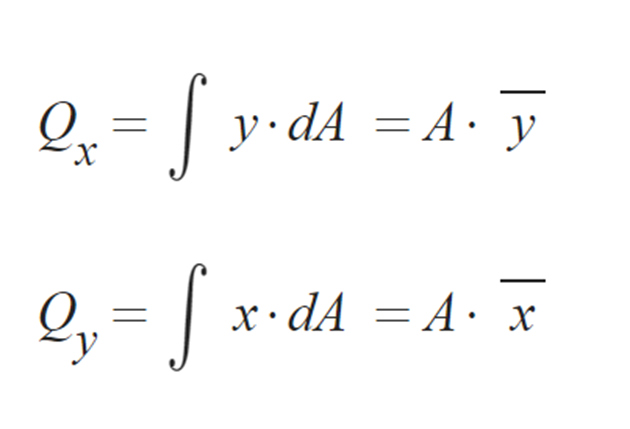
2) 단면 2차 모멘트
- 휨강성, 휨응력 산정 시 사용


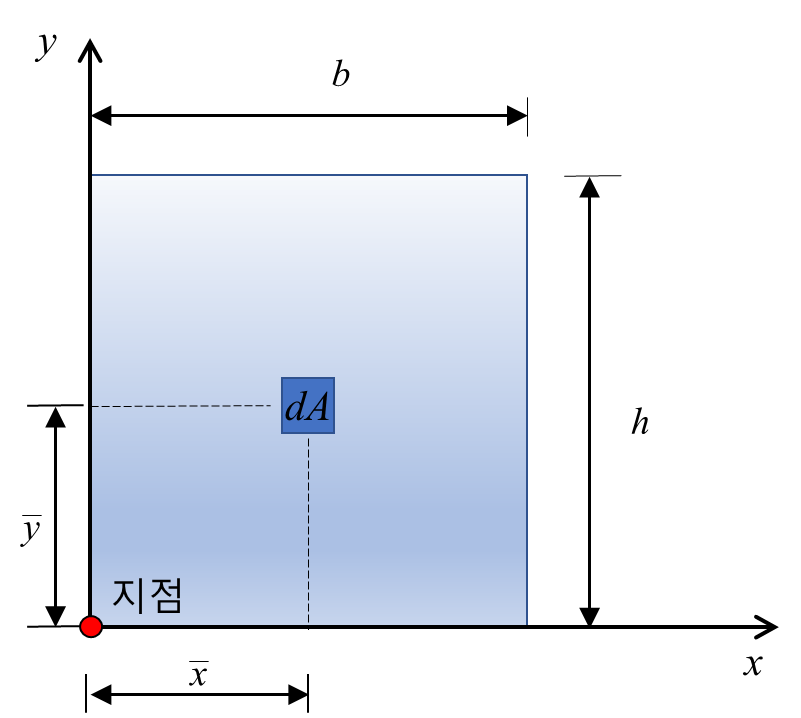
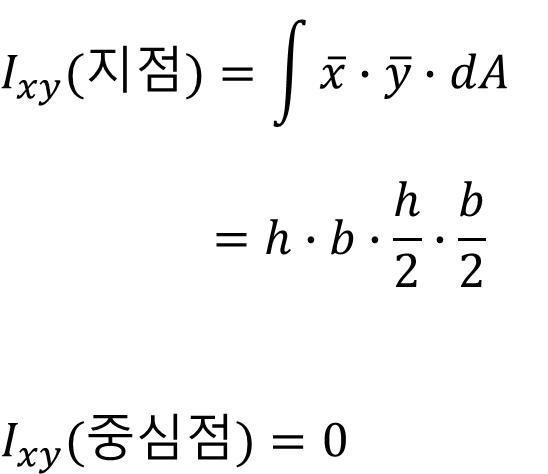

4) 극관성 모멘트
- 비틀림 산정 시 사용
- 전단 비틀림에서 비틀림 상수 J로 사용됨
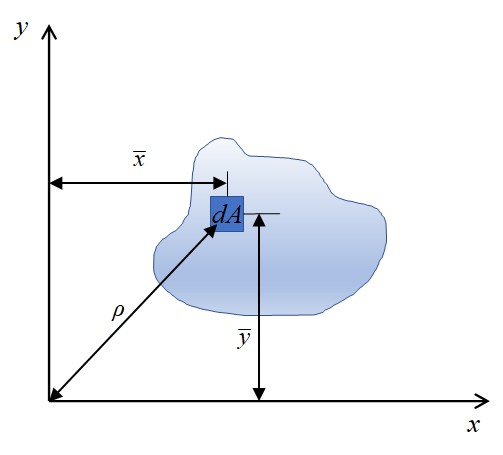
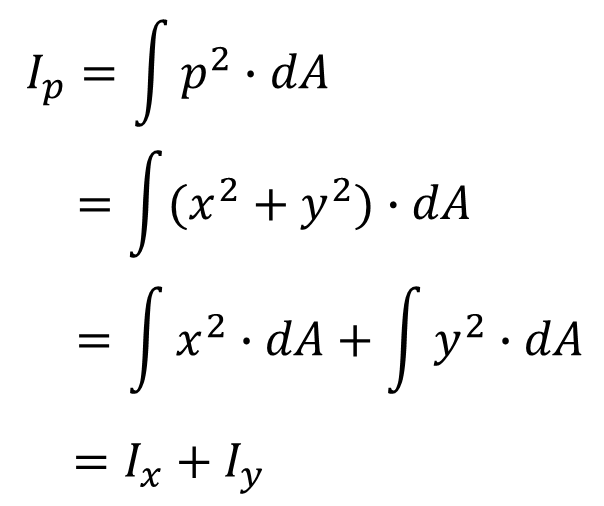

5) 주축 주단면
(1) 모어원(Mohr's Circle)
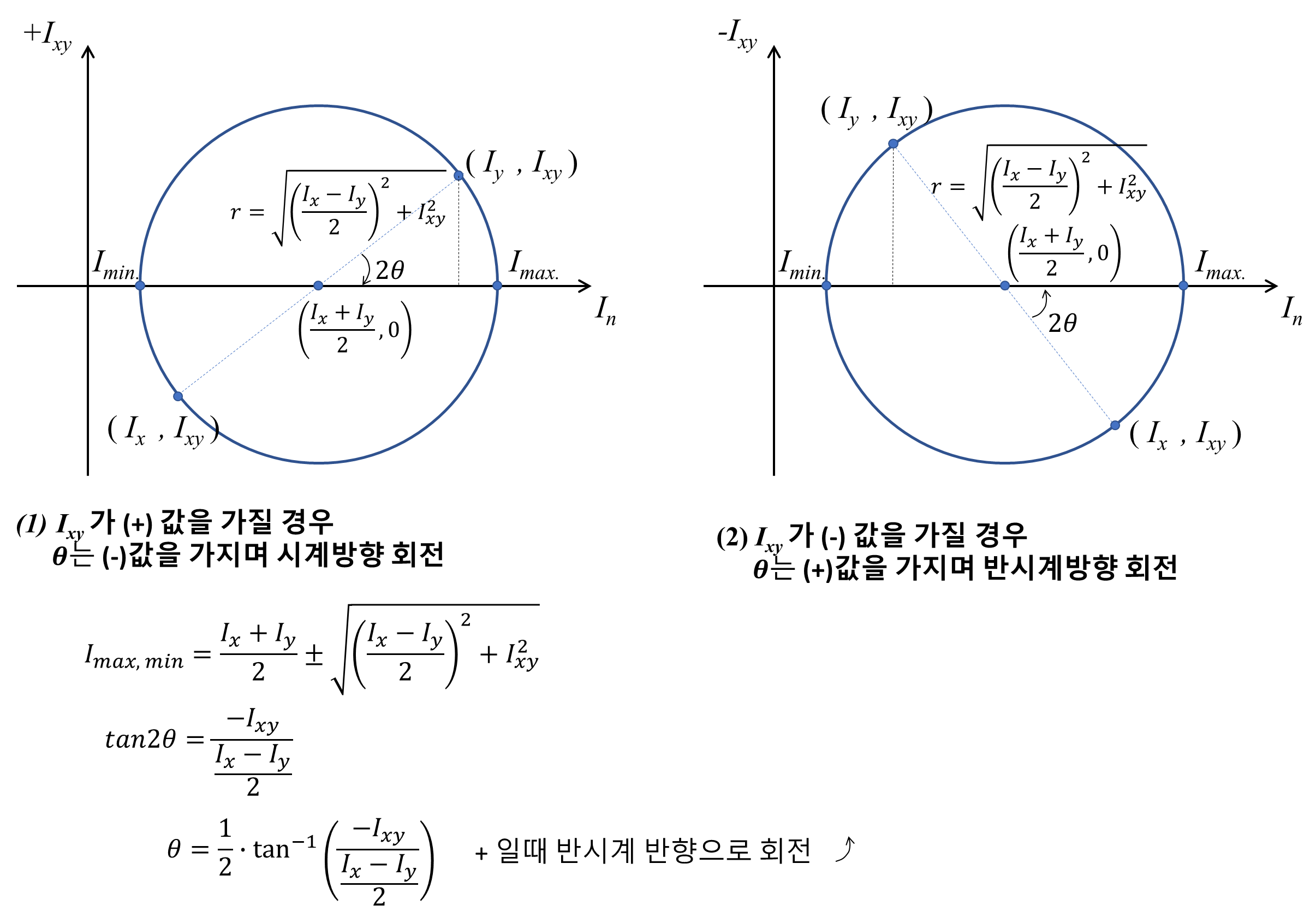
(2) 고유치 해석
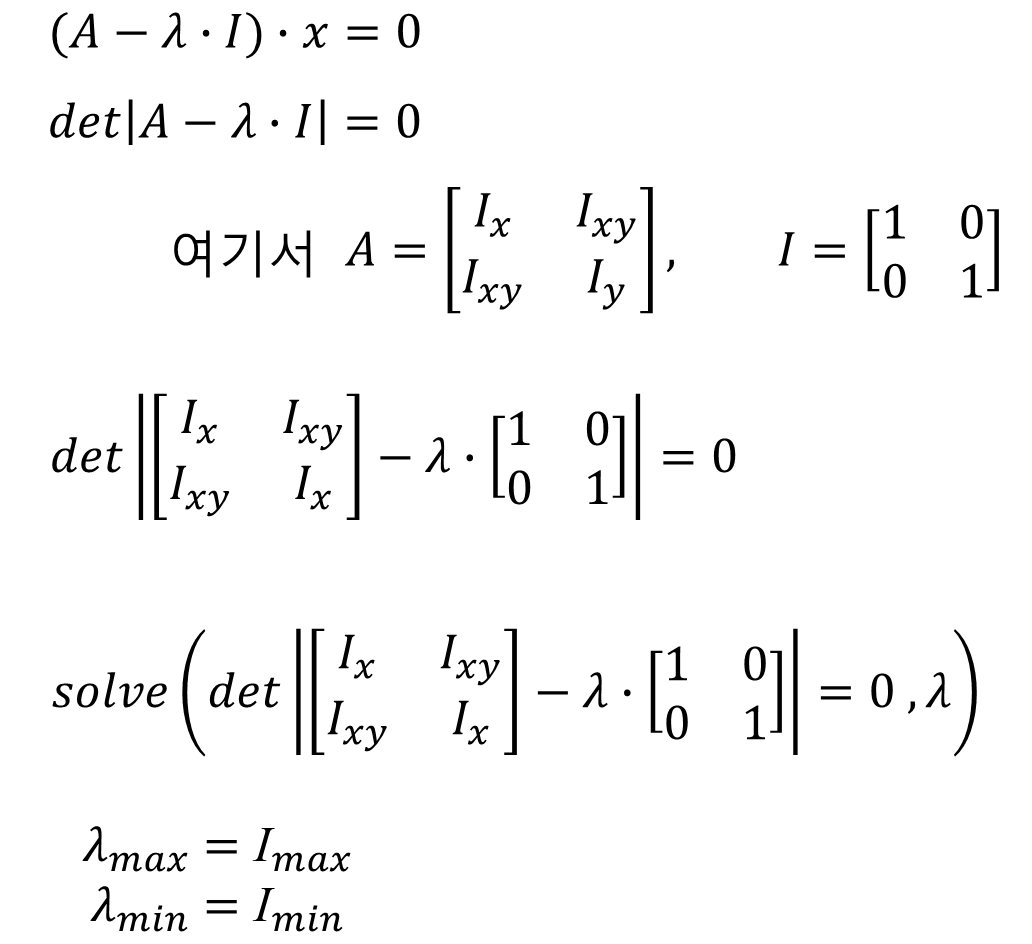
6) 탄성과 소성
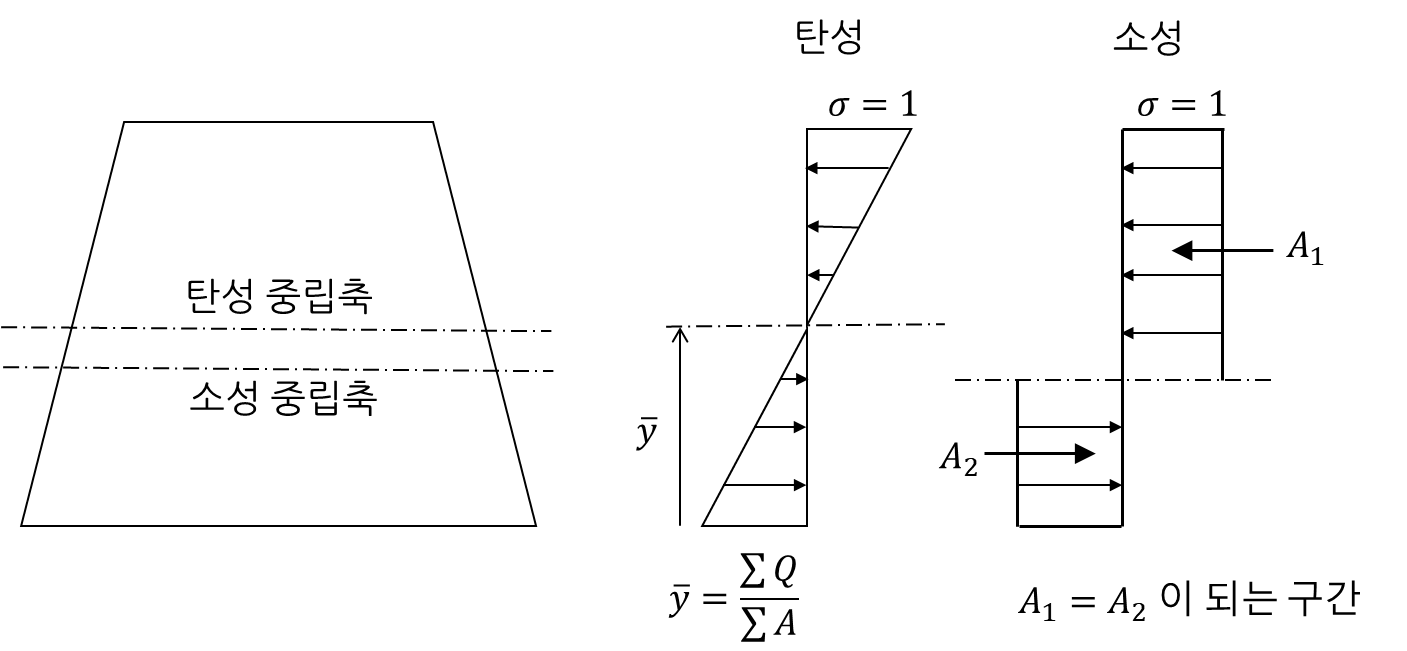
1) 탄성중립축 vs. 소성중립축
2) 탄성단면계수 vs 소성단면계수
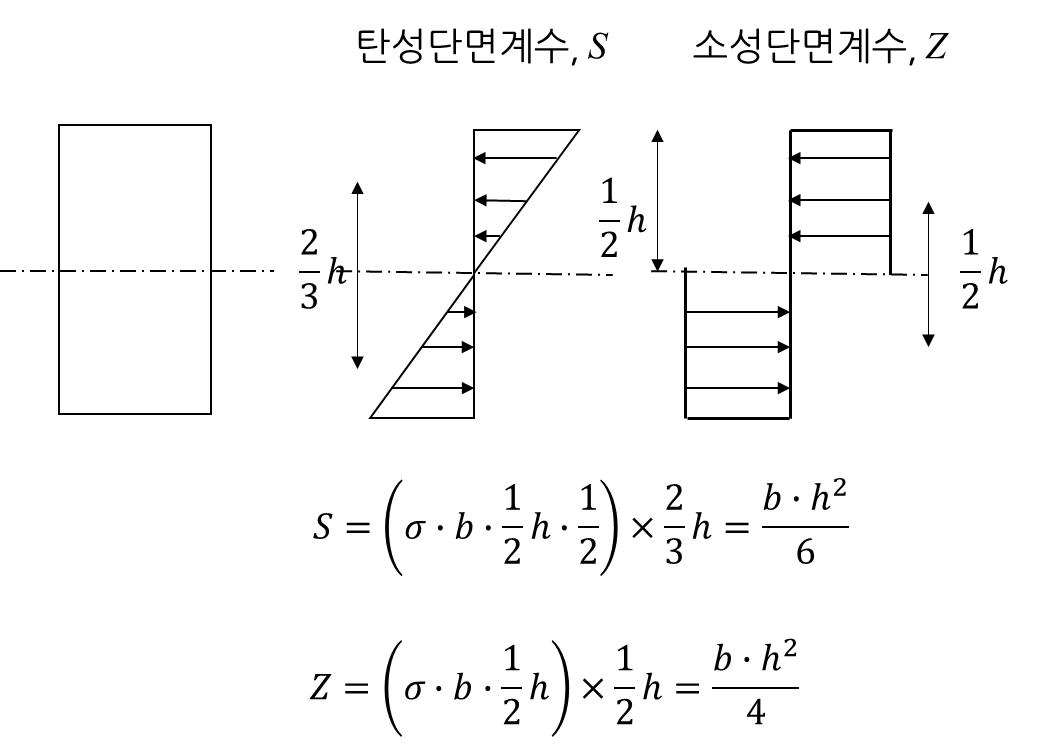
- 주요 형상별 단면의 도심축에 대한 단면성능 추가자료 첨부 예정.
표 삽입
7) 탄성계수(E)와 전단탄성계수(G)의 관계
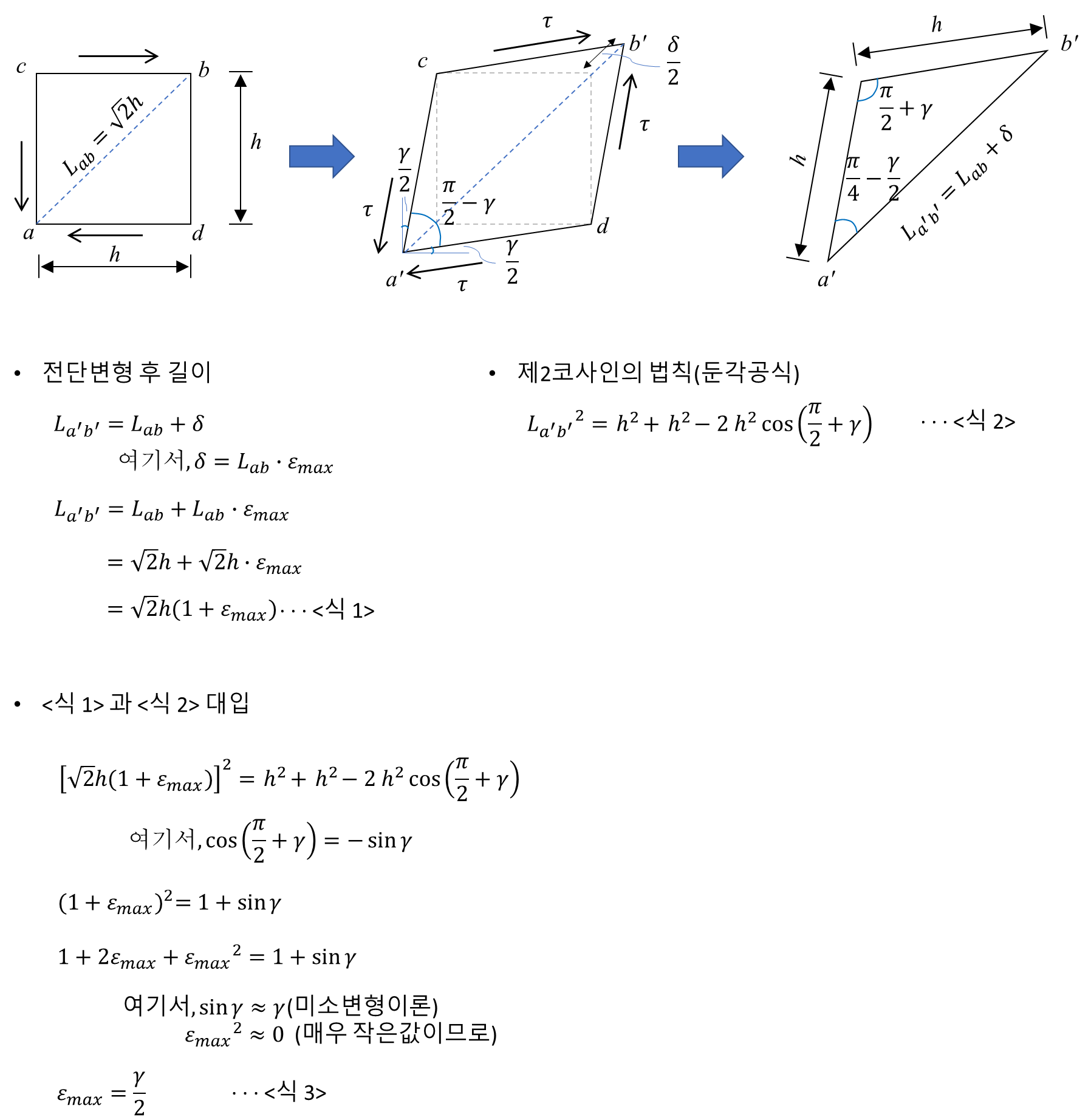

8) 비틀림
비틀림 변화율
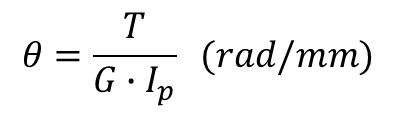
순수 비틀림
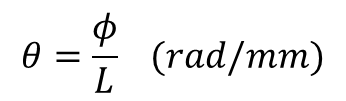
비틀림 각
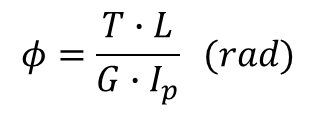
비틀림 전단응력
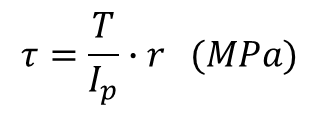
3. 힘과 응력
1) 전단과 모멘트의 관계
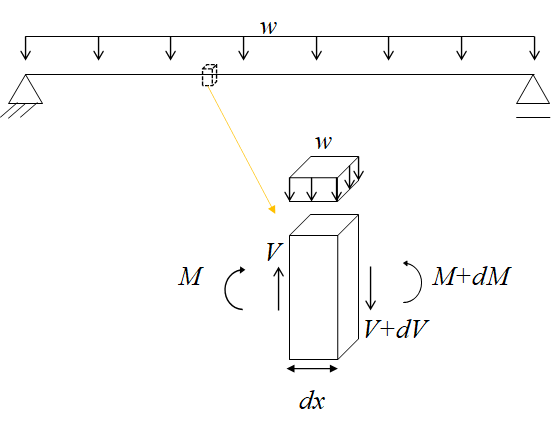
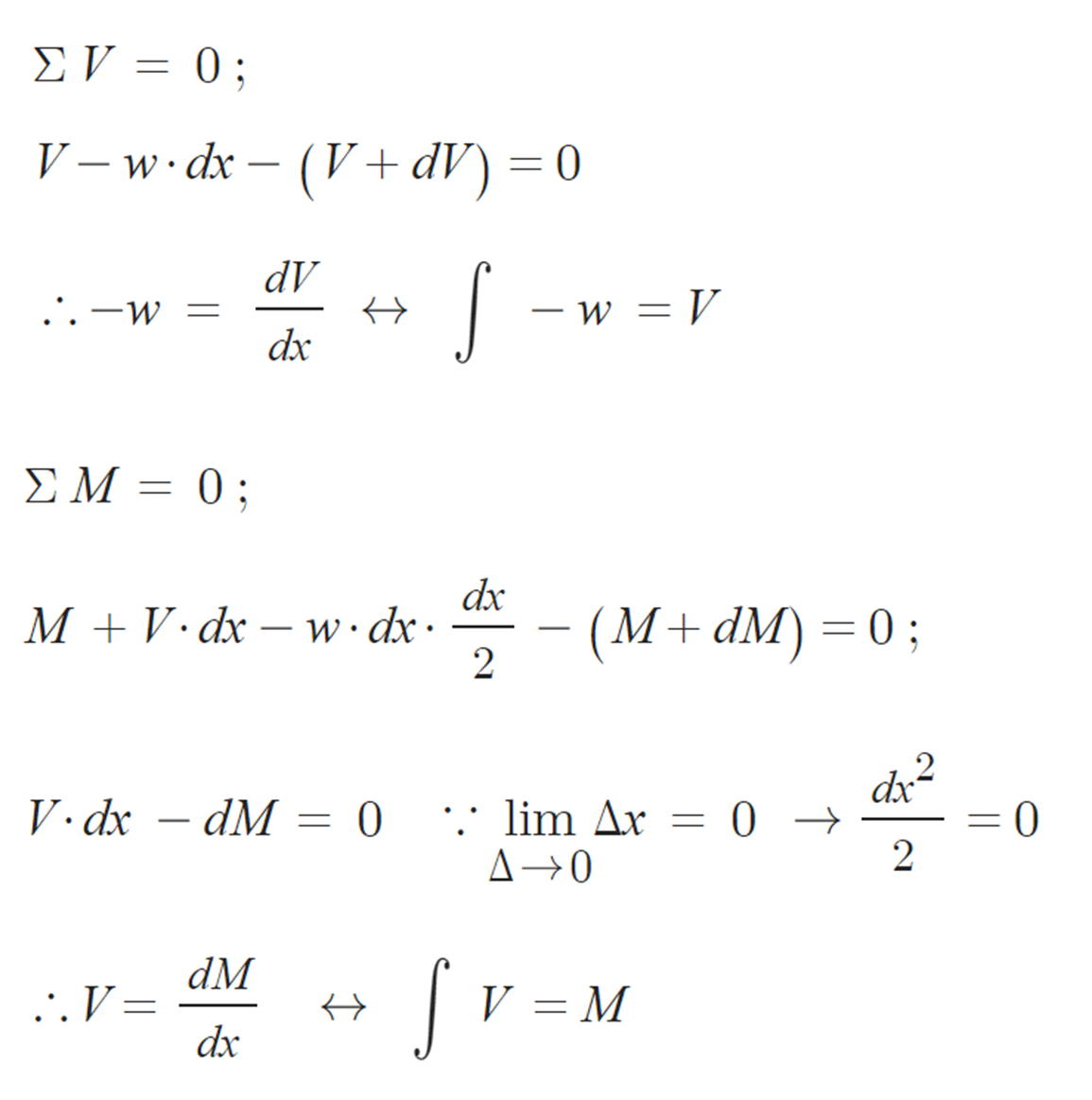
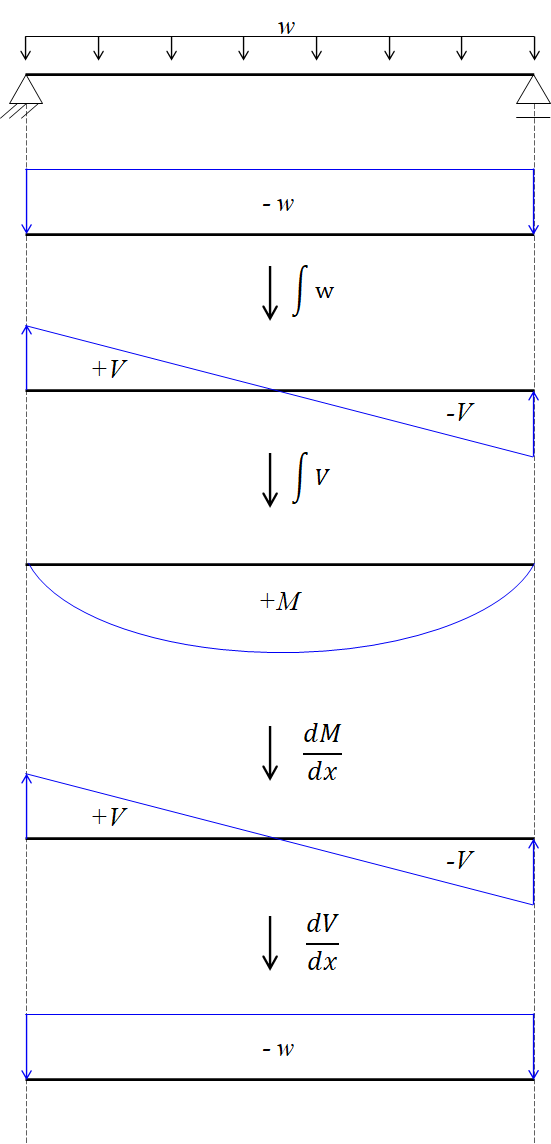
∴ 모멘트( M )을 미분하면 전단( V )이고, 전단( V )을 미분하면 하중( -w )이다.
= 하중( -w )을 적분하면 전단( V )이고, 전단( V )을 적분하면 모멘트( M )이다.
2) 훅 법칙 (Hook's Law) (출처 : 위키백과)
- 훅 법칙(영어: Hooke’s law)은 용수철과 같이 탄성이 있는 물체가 외력에 의해 늘어나거나 줄어드는 등 변형되었을 때 자신의 원래 모습으로 돌아오려고 저항하는 복원력의 크기와 변형의 정도의 관계를 나타내는 물리 법칙이다.
- 정의 : 매끈하고 평수마루 위에 용수철을 둔다. 용수철의 오른쪽 방향을 양의 x 축이라고 하자. 용수철 왼쪽 끝을 고정하고 외력이 없을 때 왼쪽 끝의 위치를 x 의 원점으로 잡자. 용수철 길이가 변했을 때, 오른쪽 끝의 x 좌표로 변형 상태를 나타내기로 한다. x > 0 이면 늘어난 것이고, x < 0 이면 줄어든 것이다. 용수철 길이의 변화가 x 일 때의 복원력을 F 로 하자. 힘이 오른쪽 방향이면 F > 0 이고, 왼쪽 방향이면 F < 0 이라 한다. 이 때, 훅 법칙은 다음과 같이 나타낼 수 있다.
F = - k·x
이 때 k 를 용수철 상수라고 부른다. 용수철 상수는 용수철의 힘 혹은 유연한 정도를 나타내는 상수로 각각의 용수철마다 다른 값을 갖는다.
3) 축응력 (Axial Stress)
① 축응력
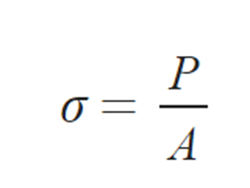
P = 축력 (Axial Froce)
A = 단면적 (Cross Sectional Area)
② δ : 축력에 의한 변위
그림 삽입 예정.
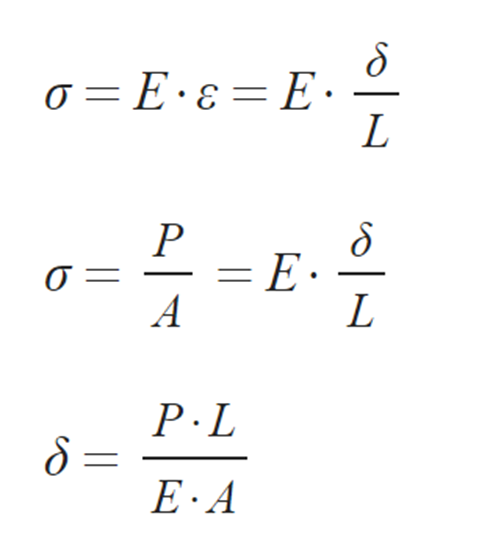
③ K : 강성도
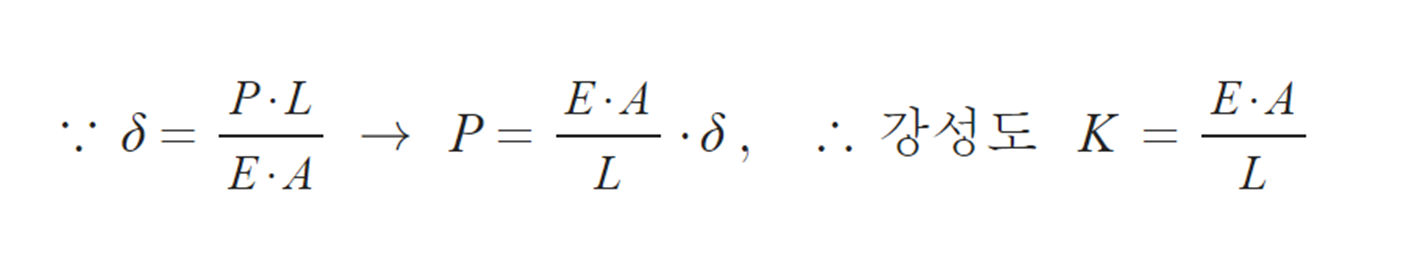
⑤ f : 유연도

⑥ δT 온도변화에 의한 팽창,수축
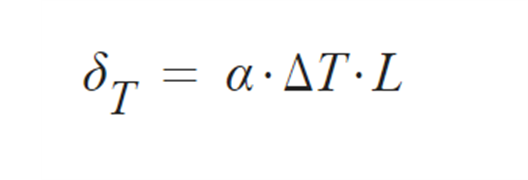
4) 휨력 (Bending Stress)
① 휨응력

M = 휨력 (Bending Moment)
y = (vertial distance away from the neutral axis)
② 유도과정 :
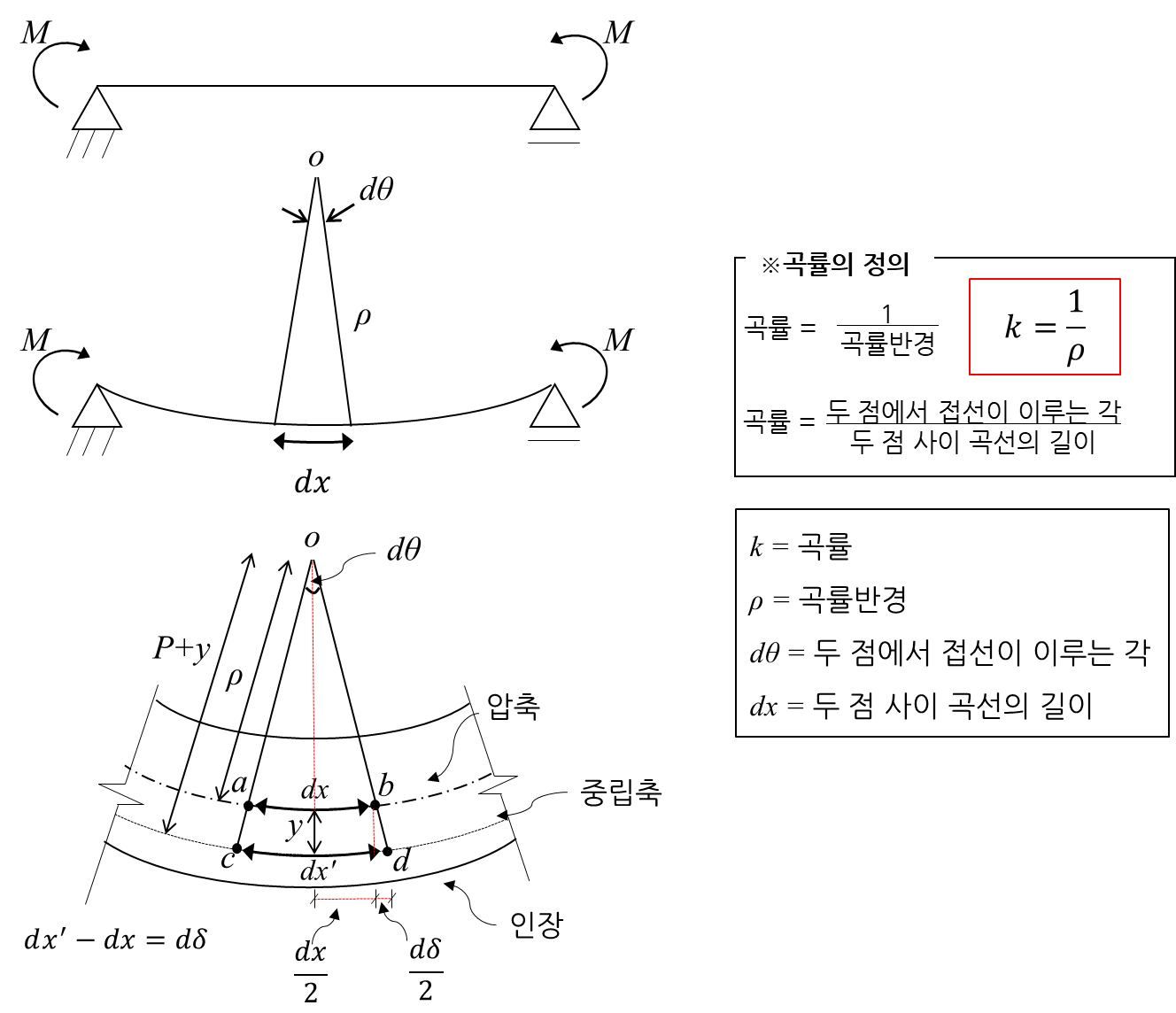

④ 변형률 ε_x 과 응력 σ_x 의 관계
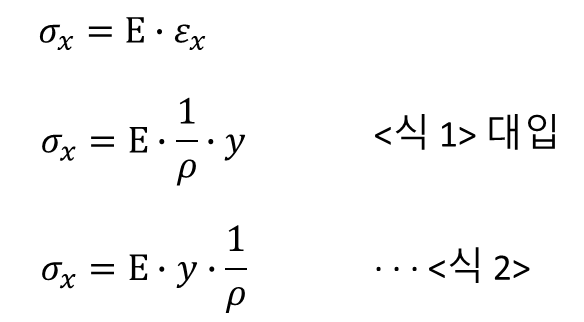
⑤ 모멘트 M 과 응력 σ_x 의 관계
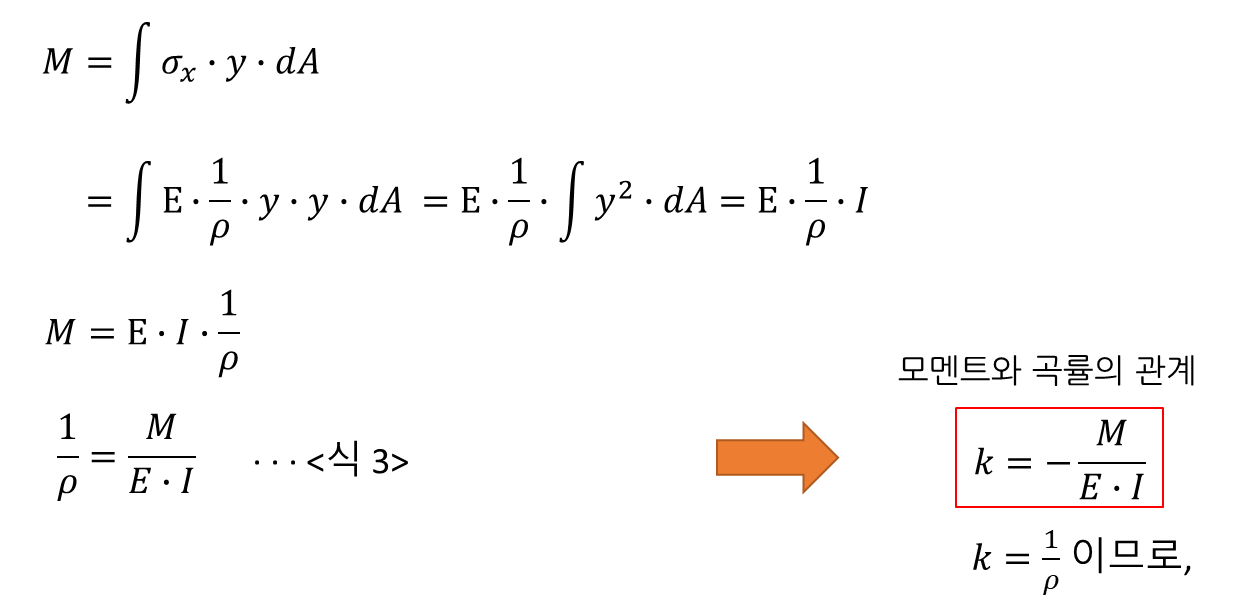
⑥ <식 2>에 <식 3>을 대입

⑦ 추가 : 탄성곡선 관계
탄성곡선 미분방정식 유도

5) 전단응력 (Shear Stress)
① 전단응력
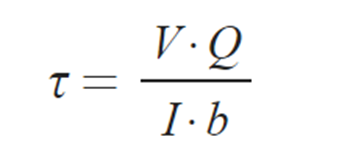
② 유도과정 :
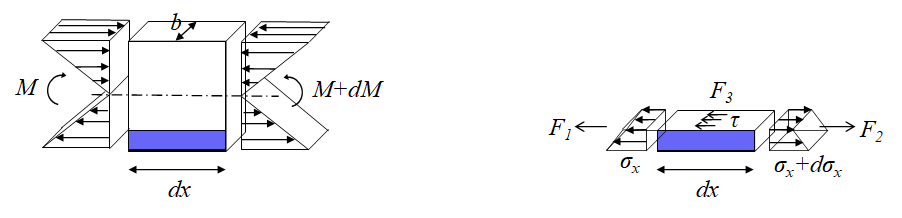
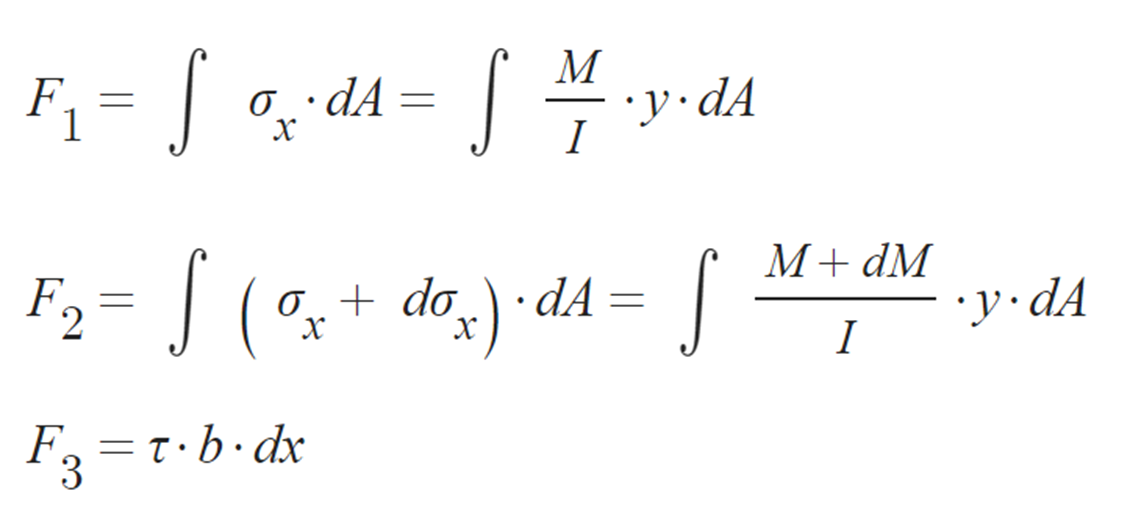
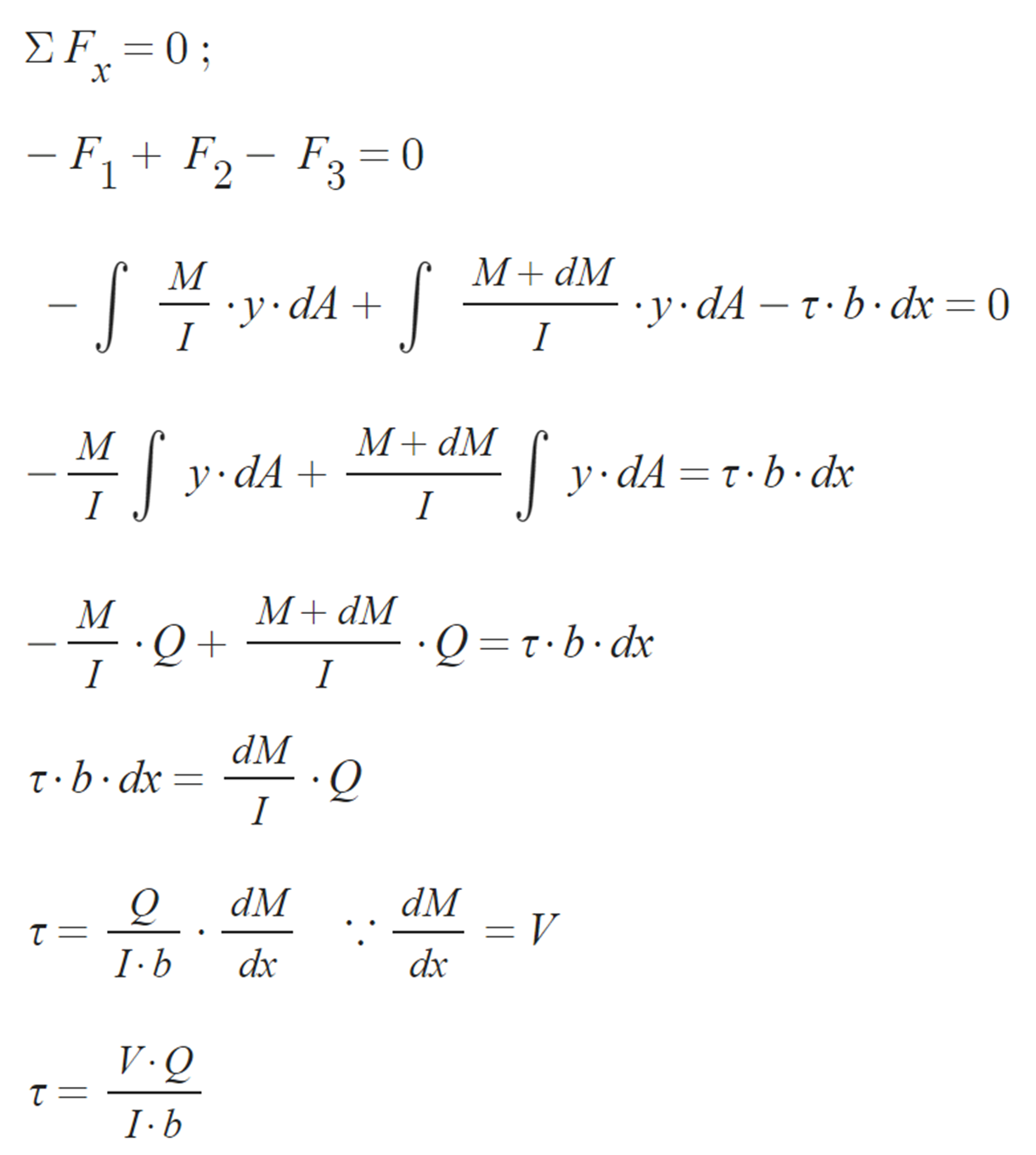
③ 전단흐름: 단위 길이당 전단력
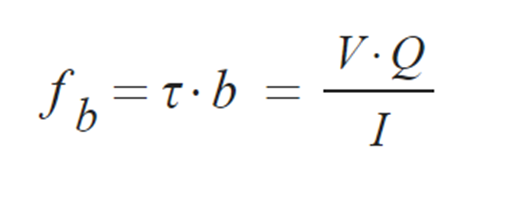
6) 전단중심 위치 산정 예제 :
전단중심 위치 산정 예제 :
7) 합성응력
4. 주응력 주축산정
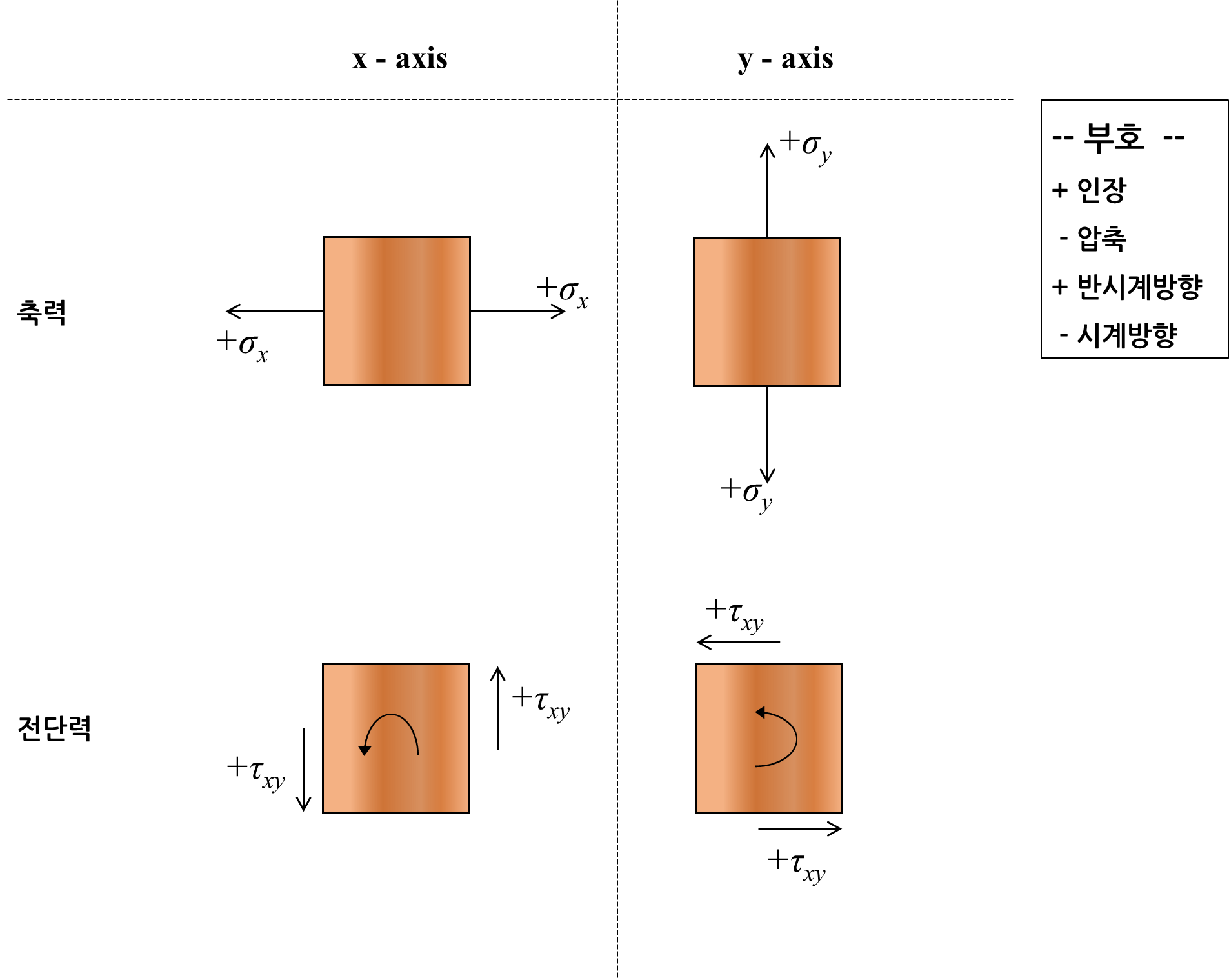

1) 모어원(Mohr's Circle)

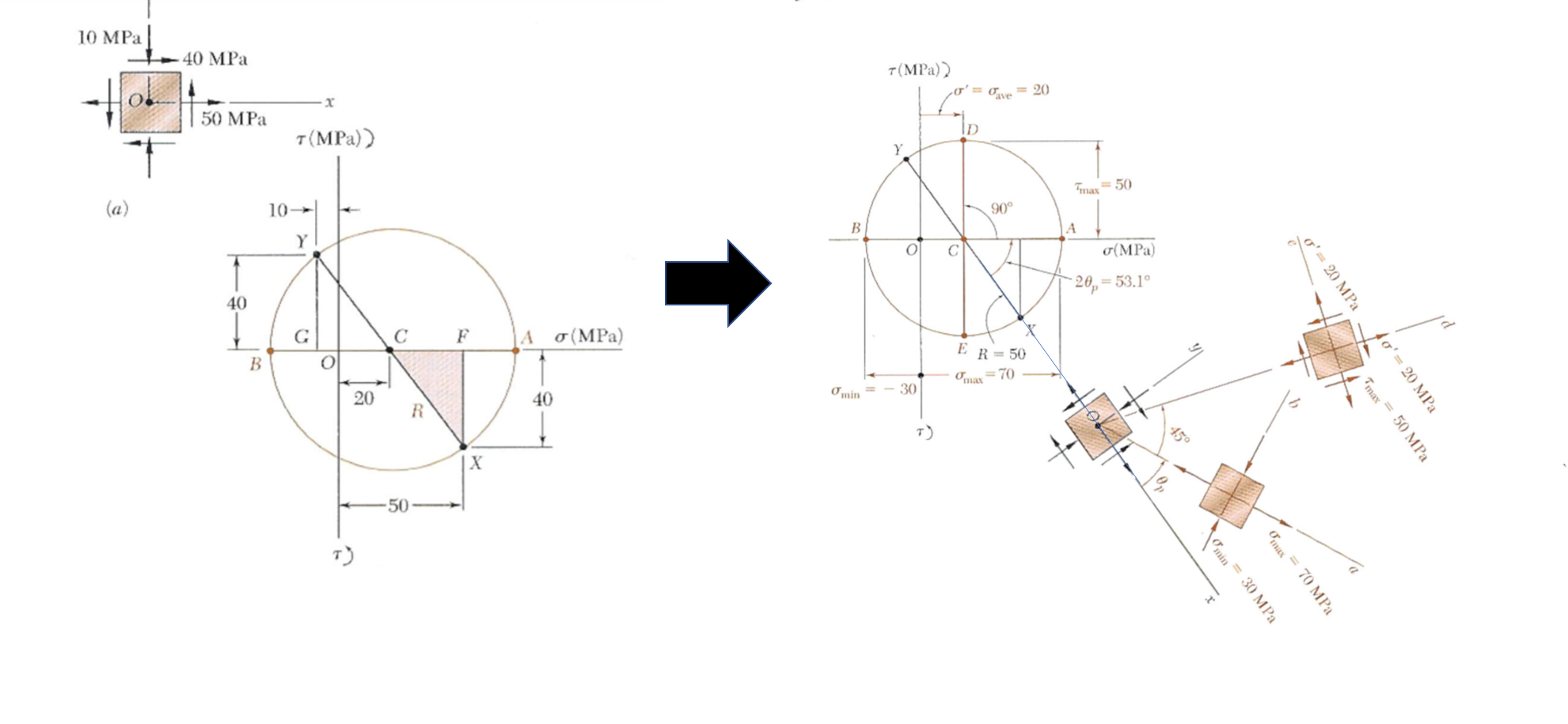
2) 고유치해석 (Eigen)
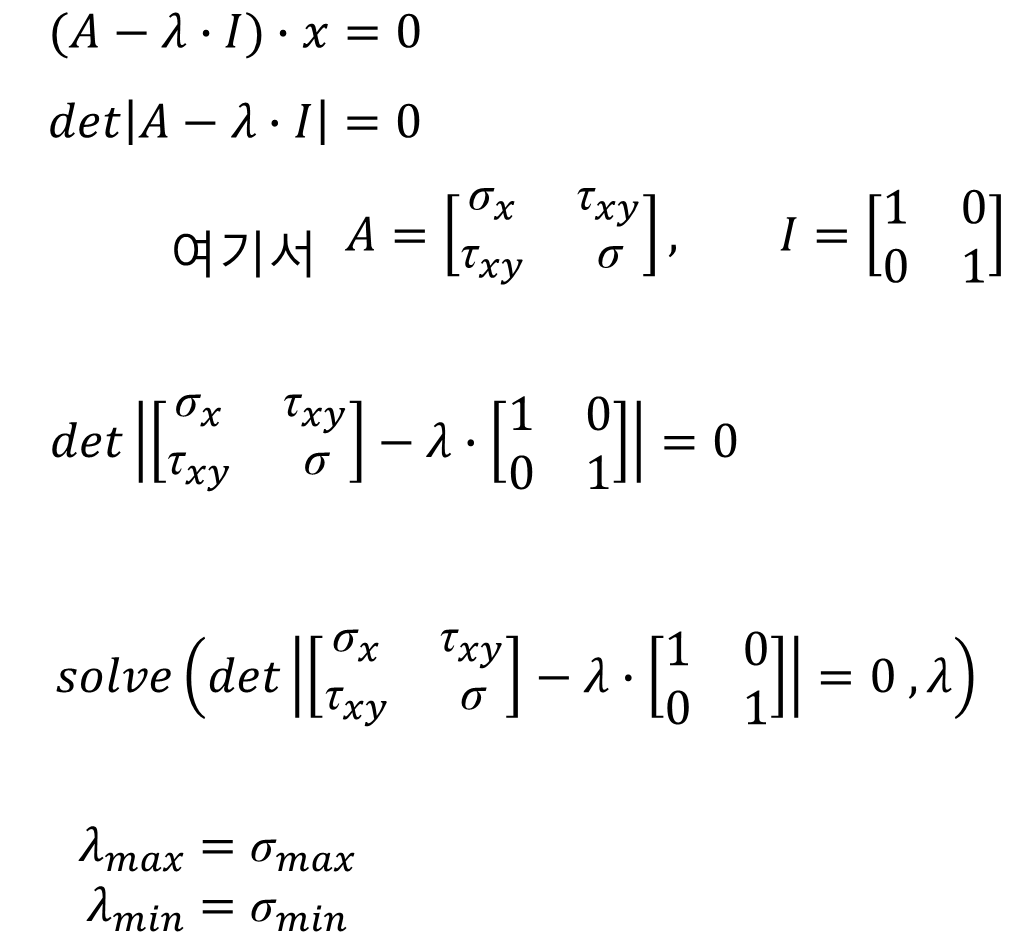
5. 좌굴안정론 (Buckling)
1) Pcr
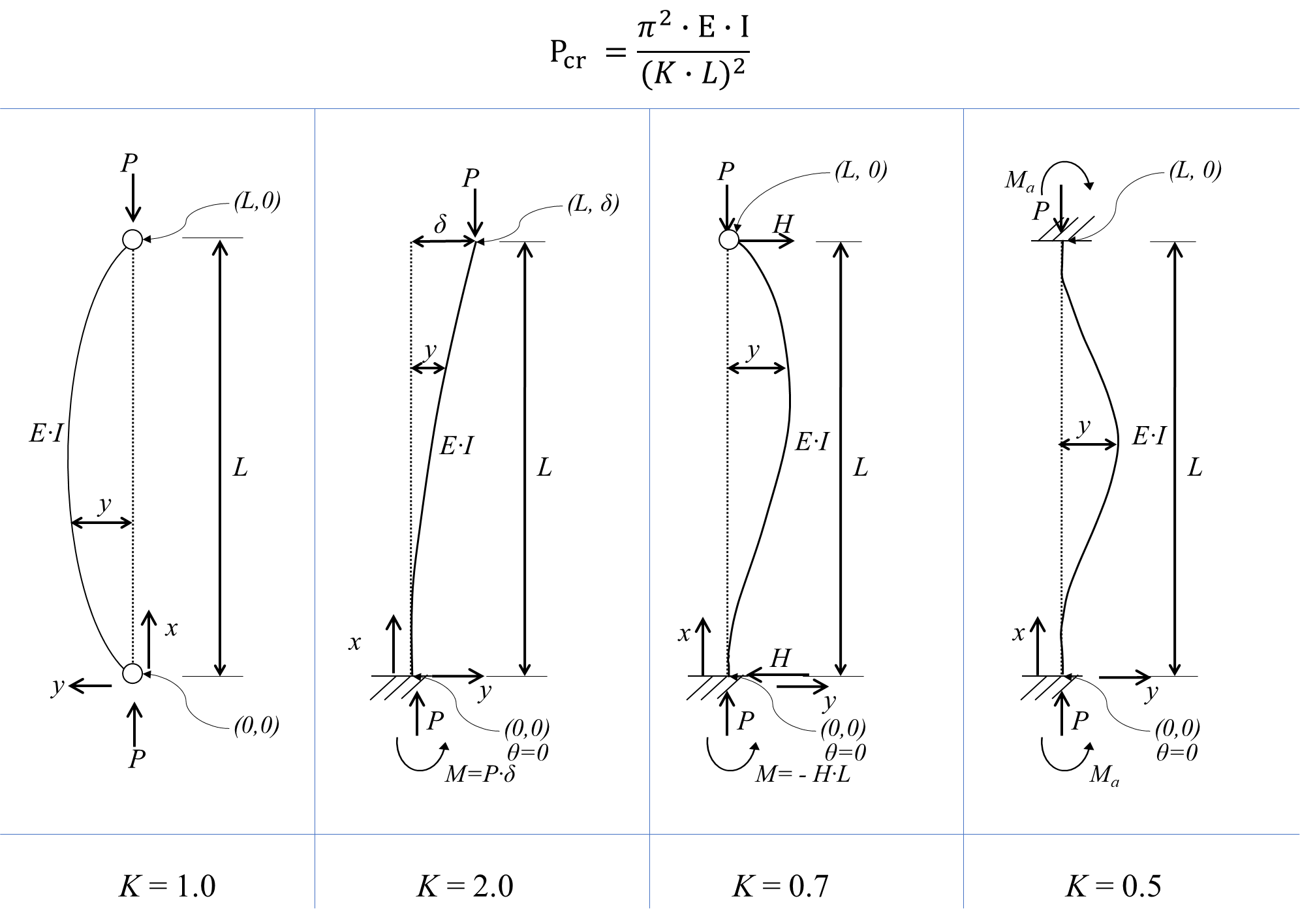
2) Pinned-Pinned 유도과정 :

2) Fixed-Free 유도과정 :
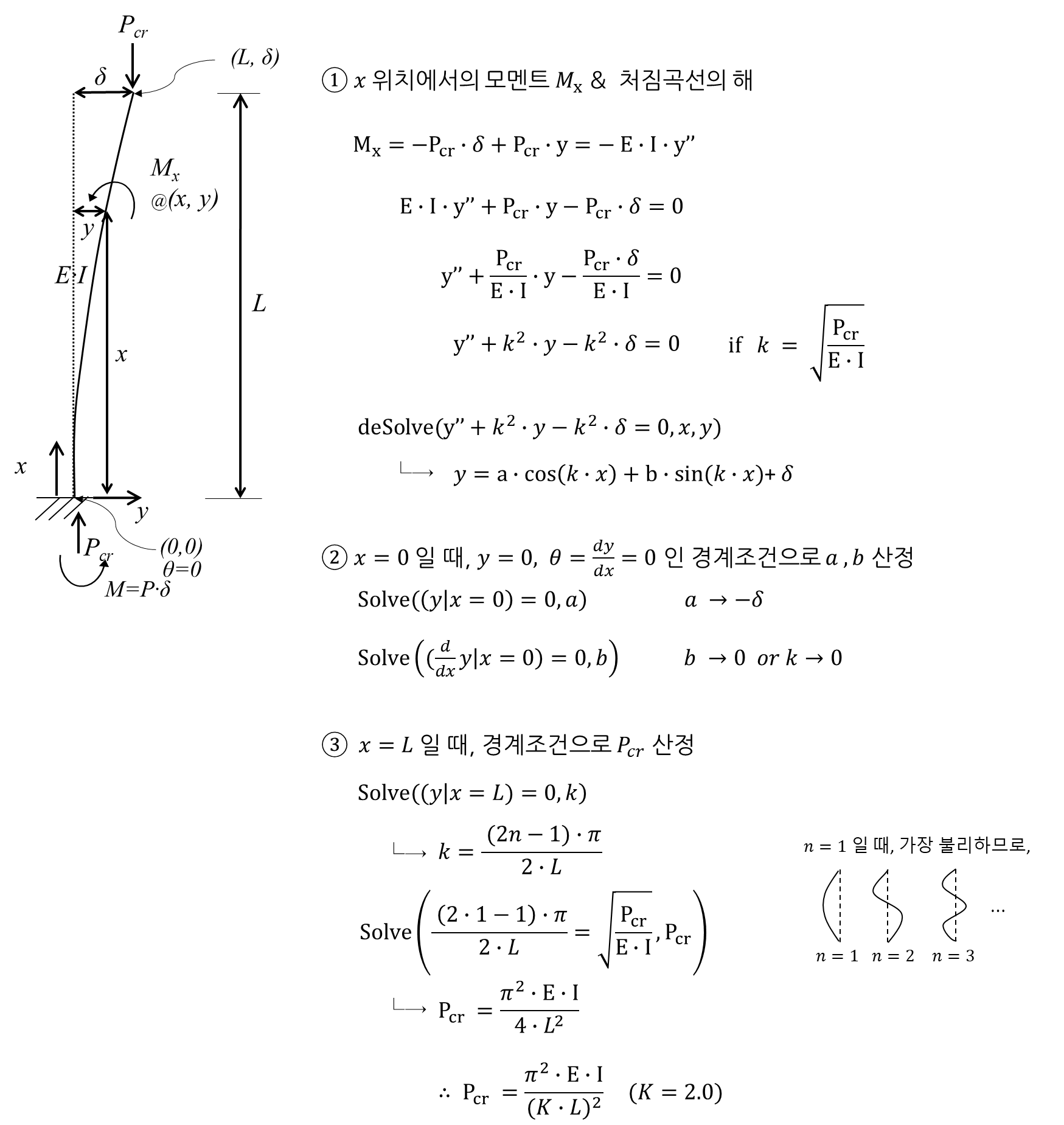
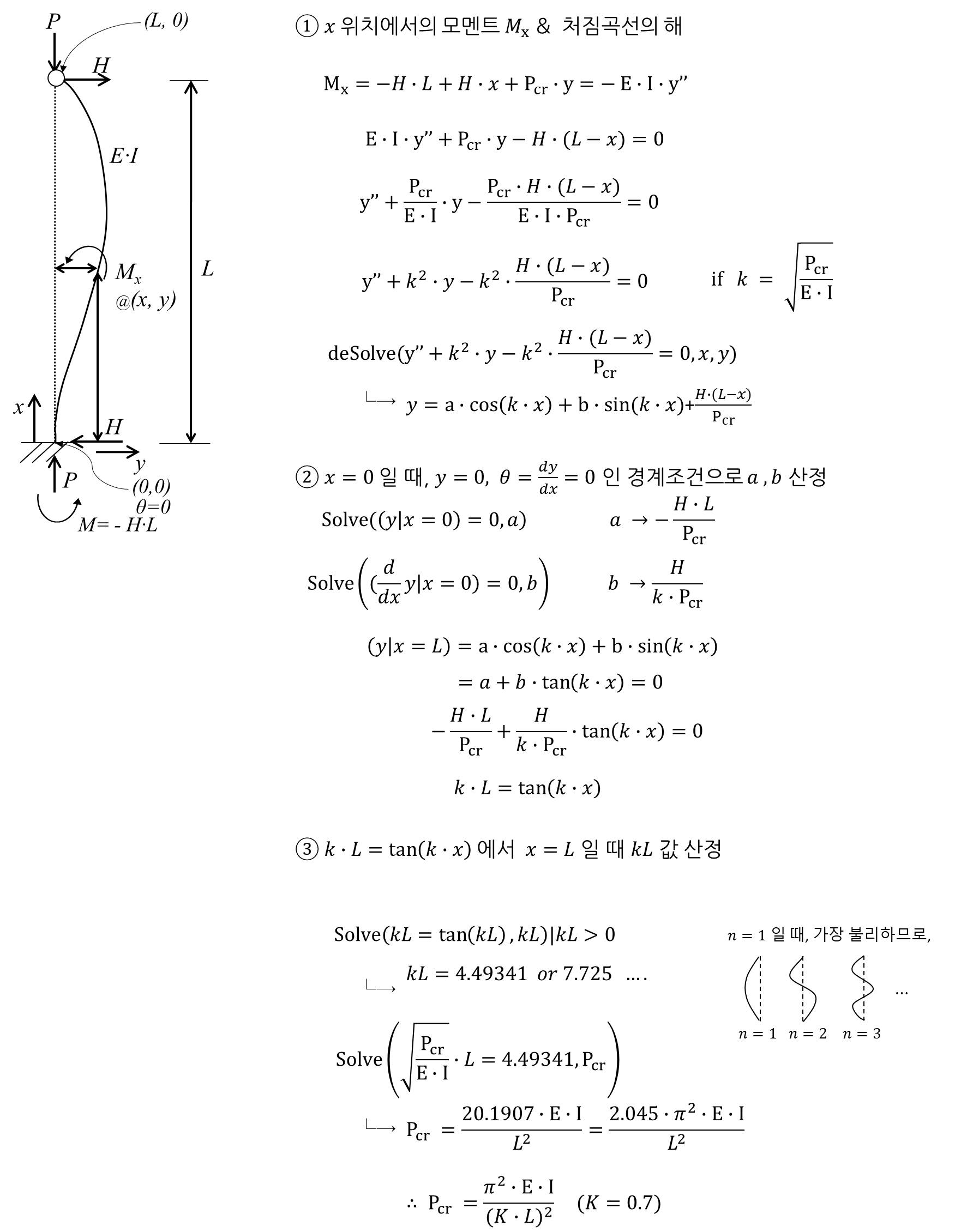
3) Fixed-Pinned 유도과정 :
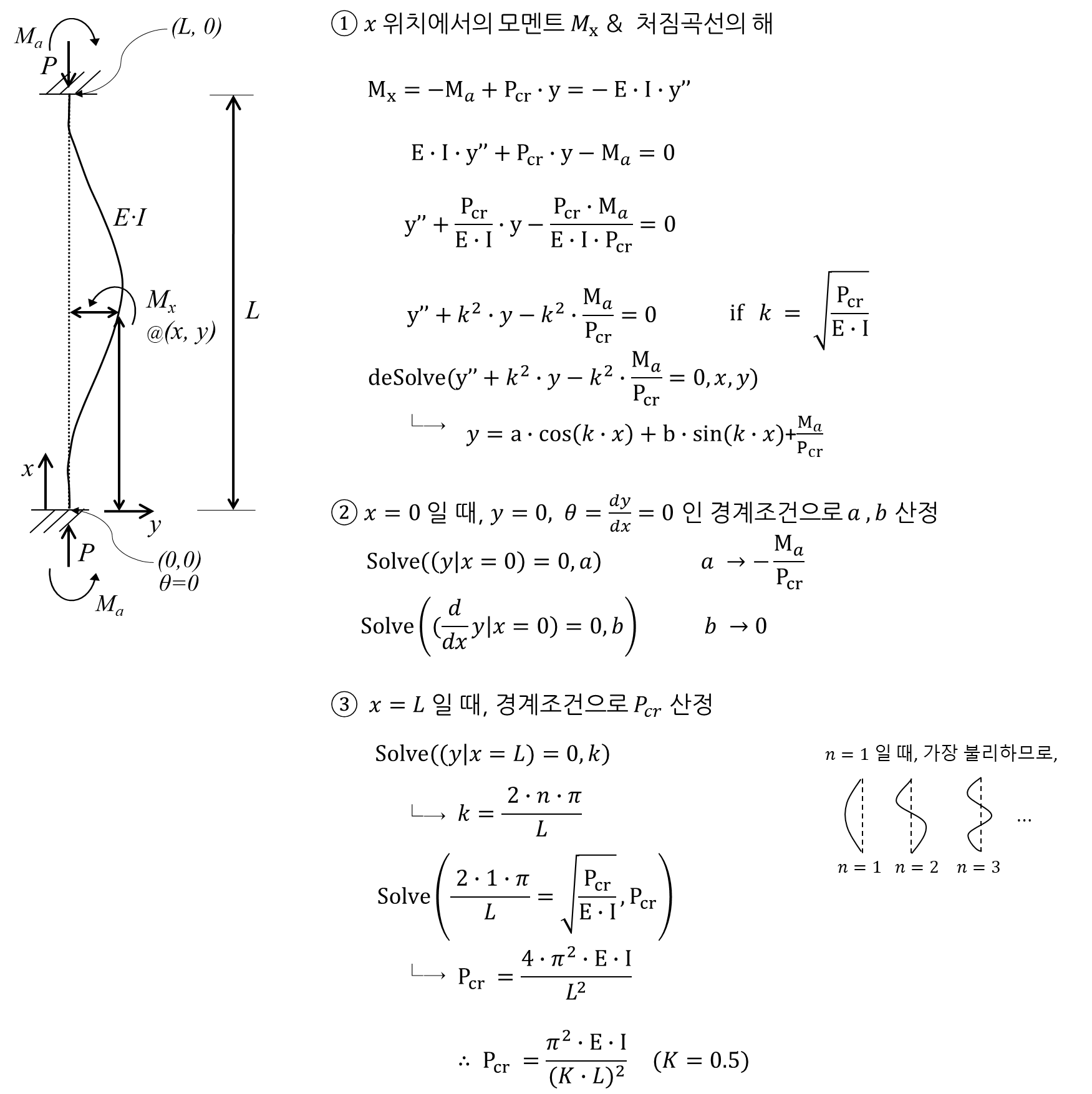
4) Fixed-Fixed 유도과정 :
6. 탄성과 비탄성
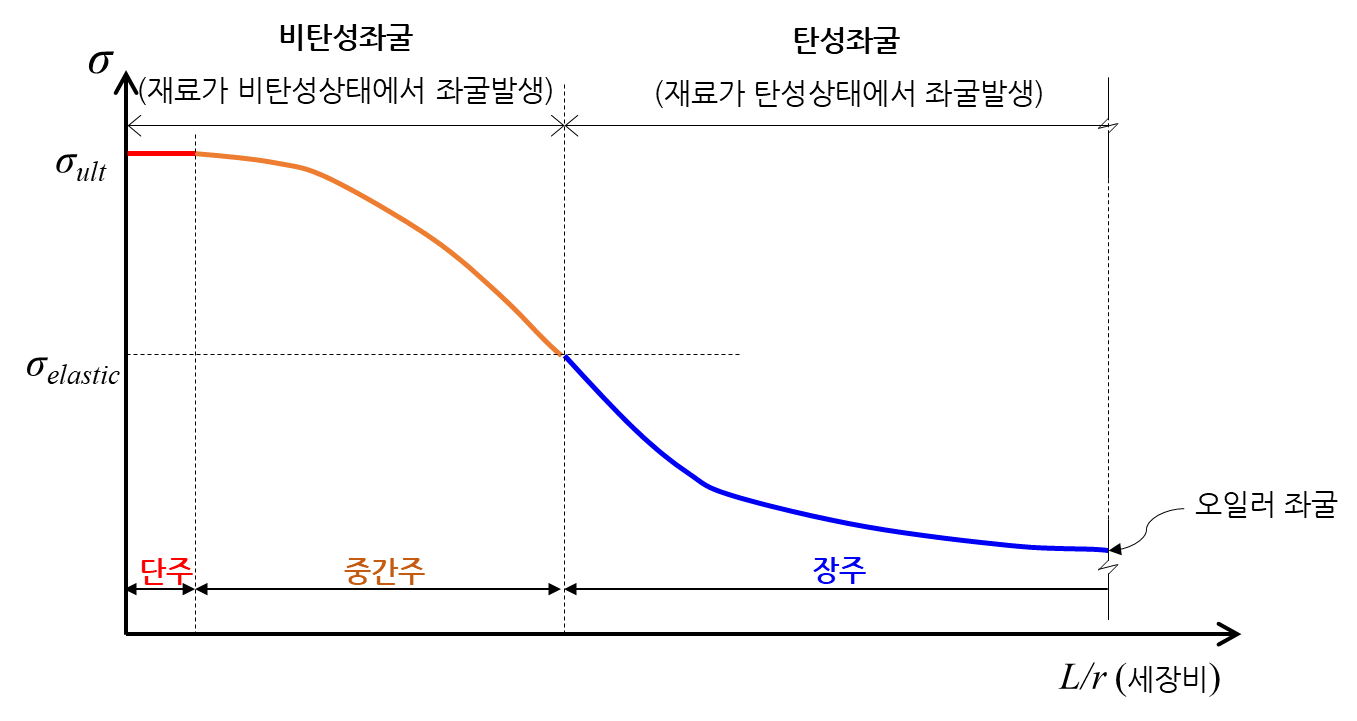
세장비에 대한 개념
r (radius of gyration )
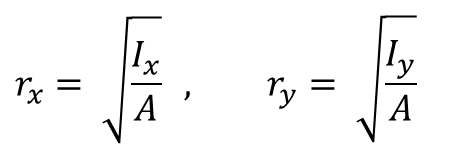
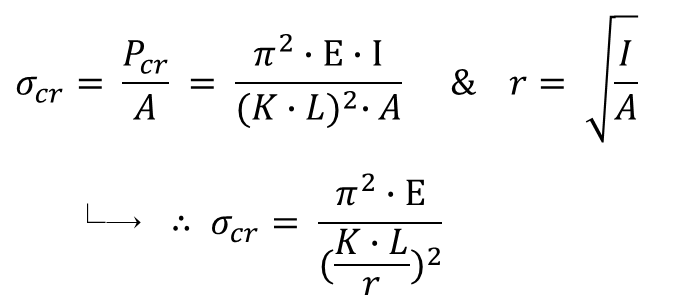
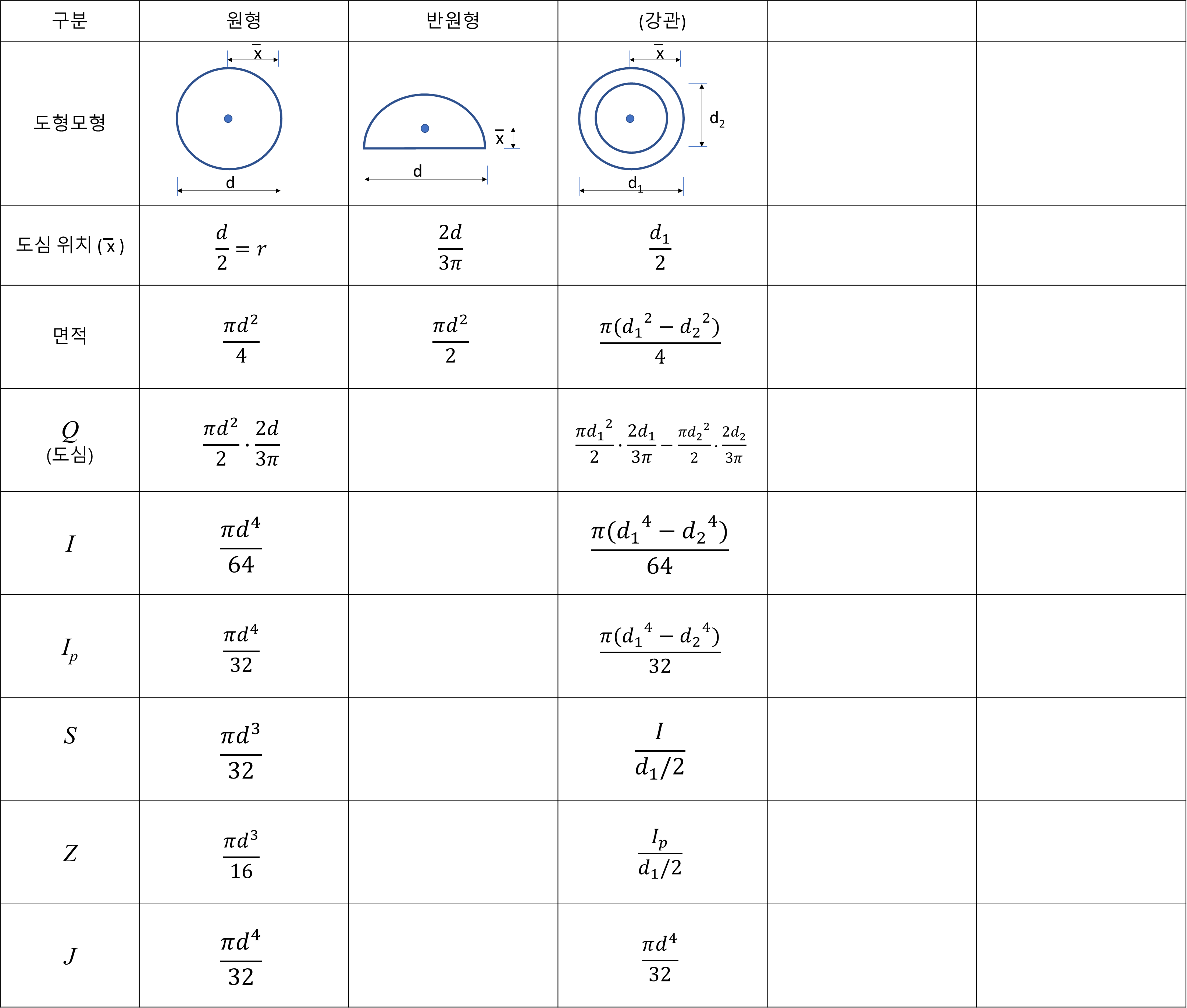
7. 주요 도형 단면의 도심위치 와 면적
형의 도심위치 및 면적

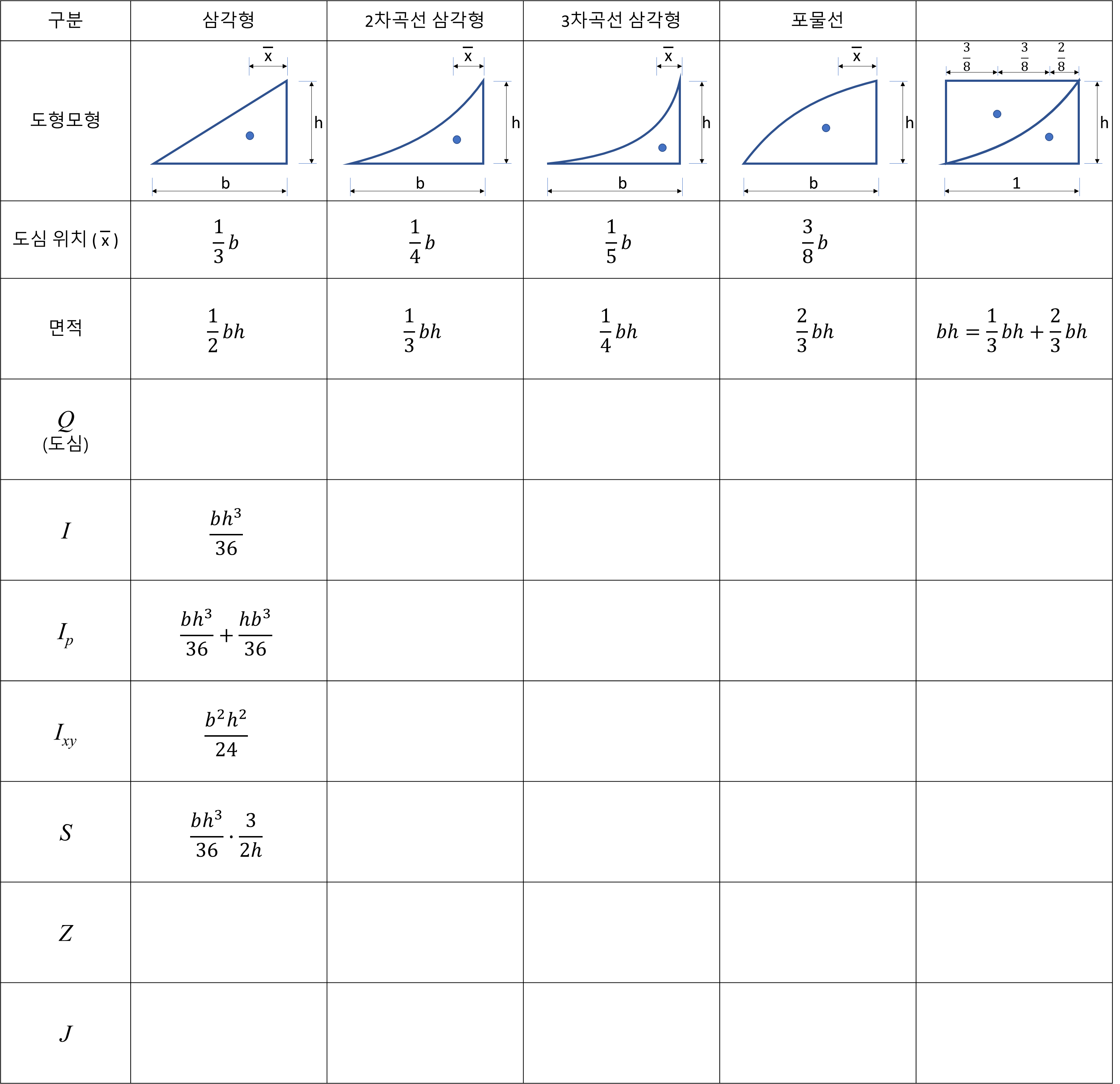
'역학 > [1] 재료역학' 카테고리의 다른 글
| [2] 재료역학 5. 좌굴안정론 (Buckling) (0) | 2023.07.17 |
|---|---|
| [2] 재료역학 4. 주응력 주축 산정 (0) | 2023.07.10 |
| [2] 재료역학 3. 힘과 응력 (0) | 2023.07.03 |
| [2] 재료역학 2. 단면의 성질 (0) | 2023.06.30 |
| [2] 재료역학 1. 고유치 해석 (0) | 2023.06.30 |



