각 자유도에 절점평형 방정식을 세우고, 평형매트릭스 A를 이용
역행렬을 산정하는 과정이 필요하므로, 복잡한 구조물일 경우 계산이 힘듦.
개요
절점과 자유도
절점 : 평형방정식이 수립되고 변위가 구해지는 점
자유도 : 그 절점에서 발생가능한 변위의 수
(그림)
부재력
(그림) 축하중을 받을 시 + 전단력, 모멘트를 받을 시
1. 부재유연도 작성
(1) 적합조건 : [e] = [A]T x [d] e = displacement or deflection
A = 방향성에 대한 매트릭스
(2) 탄성조건 : [Q] = [S] x [e] → [Q] = [S] x [A]T x [d] [S] = 부재별 강성매트릭스
- 축력일 시

- 모멘트일 시
처짐각 방정식에 의해
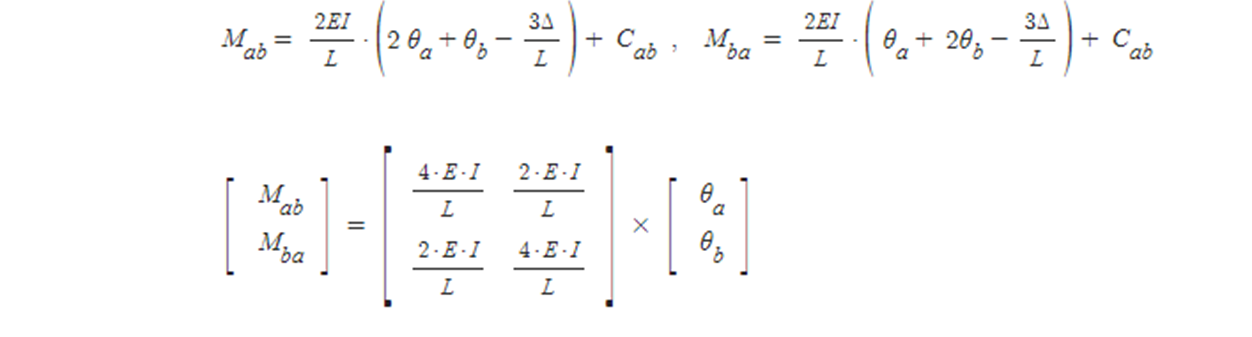
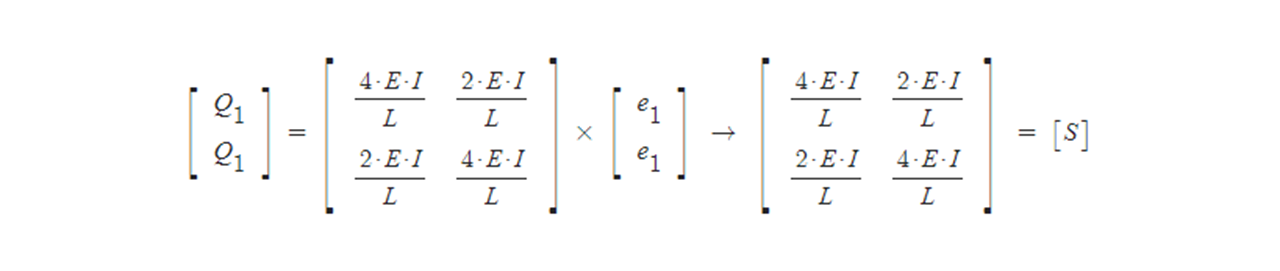
(3) 평형조건 : [P] = [A] x [Q] → [P] = [A]x[S]x[A]T x [d]
[d] = [K]-1 x [P] ∵ [K] = [A] x [S] x [A]T : 구조물 강성매트릭스
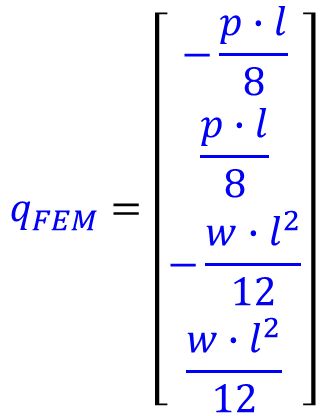
부재 내부에 하중 [qFEM] 있을 시 -> 절점하중으로 치환
[Po] = [A] x [Q]
[P] = [Po] - [A] x [qFEM]
[Q] = [S] x [A]T x [d] + [qFEM]

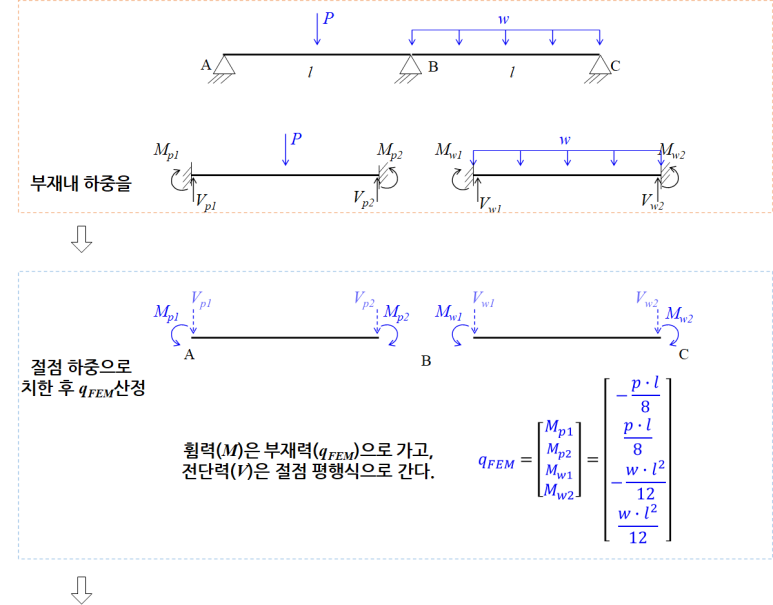
지점 침하[qΔ]가 있을 경우
[P*] = [P] - [A] x [qΔ]
[Q] = [S] x [A]T x [d] + [qFEM]+[qΔ]

반력 구하기

-------------------------------------------------------------------------------------------------------------------------------
<풀이방법>
1. 자유물체도 (부재력, 자유도)
2. 절점평형방정식 산정, A x Q = P
자유도 움직임 갯수만큼의 식 산정
자유도 1 : ΣH@A = 0; 자유도 1 식 : A11 · Q1 + A12 · Q2 +A13 · Q3 +A14 · Q4 + · · = P1
자유도 2 : : A21 · Q1 + A22 · Q2 +A23 · Q3 +A24 · Q4 + · · = P1
자유도 3 : : A31 · Q1 + A32 · Q2 +A33 · Q3 +A34 · Q4 + · · = P1
: :
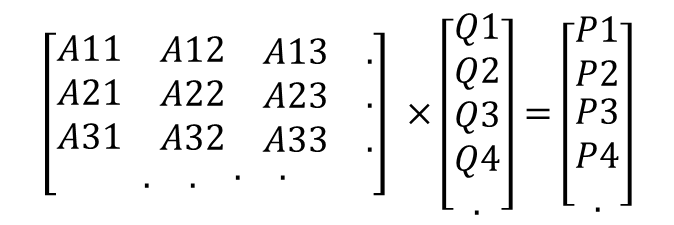
3. 절점평형방정식을 매트릭스로 변환, A x Q = P

[Po] = [A] x [Q]
부재내 하중이 있을 경우 (qFEM)
[P] = [Po] - [A] x [qFEM]
지점 침하가 있을 경우 (qΔ)
[P*] = [Po]- [A] x [qFEM] - [A] x [qΔ]
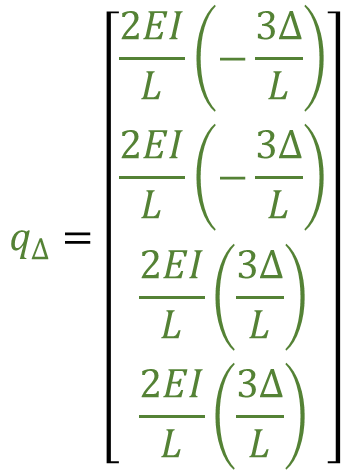
4. 전부재 강성 매트릭스, S
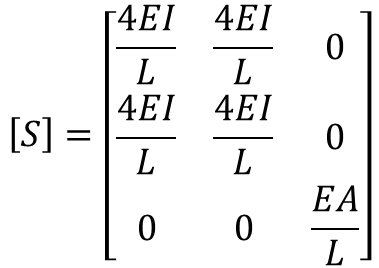
[Q] 가 n행 이면, [S] 은 n x n 행열
5. 구조물 강성 매트릭스, [K] = [A] x [S] x [A]T
6. 격점 변위 매트릭스, [d] = [K]-1 x [P]
7. 부재력 산정 [Q] = [S] x [A]T x [d]
or
[Q] = [S] x [A]T x [d] + [qFEM] + [qΔ]
왜 qFEM을 d 구할 때 빼놨다가 Q구할 때 다시 넣는 건지 이해 못함....
- 아 처음 절점 방정식 구할 때 넣으면 부재내 하중이 - 값으로 들어가는 구먼
8. 각 절점 평형 식으로 각 절점에서의 반력 산정 후 S.F.D & B.M.D 작성
예)
'역학 > [2] 구조역학' 카테고리의 다른 글
| [3] 구조역학 1. 부호의 규정 및 정정과 부정정 (0) | 2023.03.07 |
|---|---|
| [3] 구조역학 7. 부정정 구조물의 해석(모멘트분배법) (0) | 2023.01.08 |
| [3] 구조역학 5. 부정정 구조물의 해석 (처짐각법) (0) | 2022.12.04 |
| [3] 구조역학 4. 부정정 구조물의 해석 (에너지법) (1) | 2022.12.04 |
| [3] 구조역학 3. 정정 구조물의 탄성 변형 (처짐 및 처짐각 산정) (0) | 2022.05.11 |



