#에너지법
에너지 법으로 정정구조물 및 부정정구조물의 해석을 할 수 있다.
1) 정의
(1) 카스틸리아노제1의 정리
① 제1정리–구조물의 어떤 점에 힘이나 모멘트가 작용했을 때, 그 작용점에서 이들로 인한 처짐이나 회전각은 변형에너지를 작용하는 힘이나 모멘트로 편미분한 것과 같다. (출처: 대한건축학회 건축용어사전)
(2) 카스틸리아노제2의 정리 (최소일의 법칙)
② 제2 정리–구조물에 생기는 반력은 구조물의 변형 에너지가 최소가 되도록 한다. ③ 즉 지점 반력은 변형에너지를 그 지점 반력으로 편미분할 때 0이다. ④ 최소일원리라고도 한다. (출처: 대한건축학회 건축용어사전)
③ 고려사항
- 3차부정정이하일 때 사용하면 조으당
2) 풀이방법
(1) 자유물체도로 부정정력 선정
m+f+r-2j = n차 부정정
n개의 부정정 선정
Mx, Vx, Hx , Nx
가능한 부정정력 = 반력 (MA, VA, HA)
= 내력(N1, N2, M1)
= 변위(Po, Mo) 해당 힘은 dU/dPo | Po=0 을 이용해 변위를 구함.
(2) 구하고자하는 변위 위치에 가상의 힘 적용
δ를 구하기위해 그 지점에 Po 적용
θ를 구하기 위해 그 지점에 Mo 적용
(3) 반력 선정
최대한 반력을 사용하지 않게 부재력식 산정 하기 ( = 반력을 부재력으로 둠)
반력은 부정정력을 동반함 : 예) MA = Po x L/2, VA= Po/2
(4) 구간별 부재력식 산정 (f(x) 식 )
n절점에서 ΣH=0, N1 = Nx · cosθ· + HA· · ·
ΣV=0, N2 = sinθ·Nx + Vx· · ·
n+1절점에서 ΣH=0, N3 = Vx · cosθ · · ·
.
.
.
M1 = VA ·x · · ·
M2 = VA ·(L+x) · · · · · ·
M3 = · · ·
.
.
.
(5) 에너지식 산정
Total Energy Combined
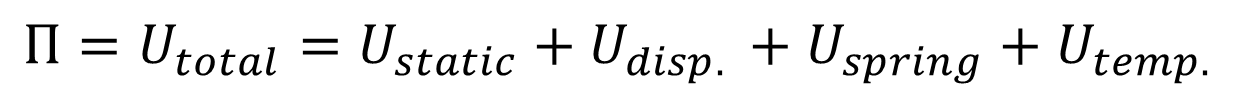
- Ustatic : Static Energy
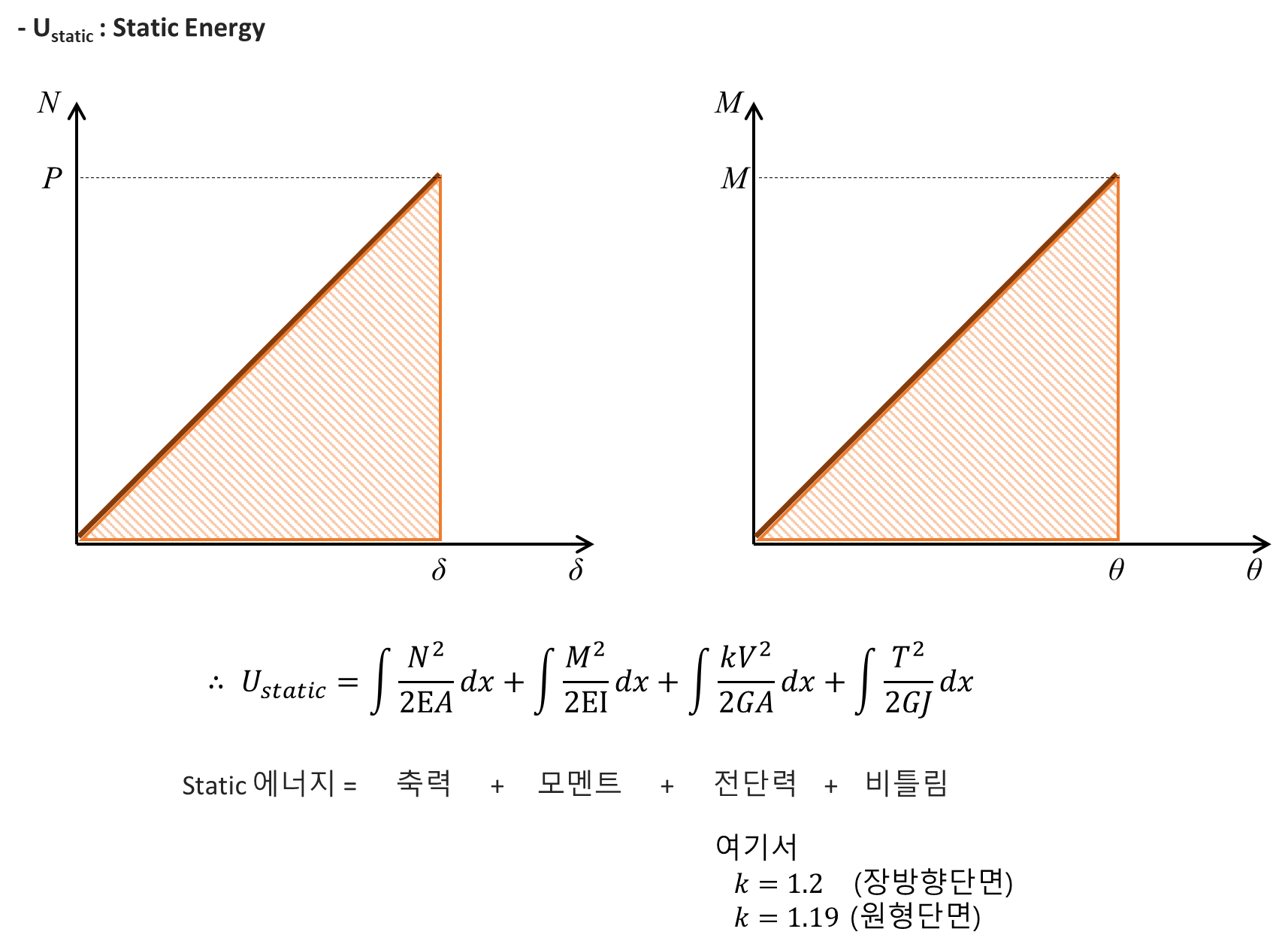
- Ud : Displacement Energy (침하, 회전, 축변형)
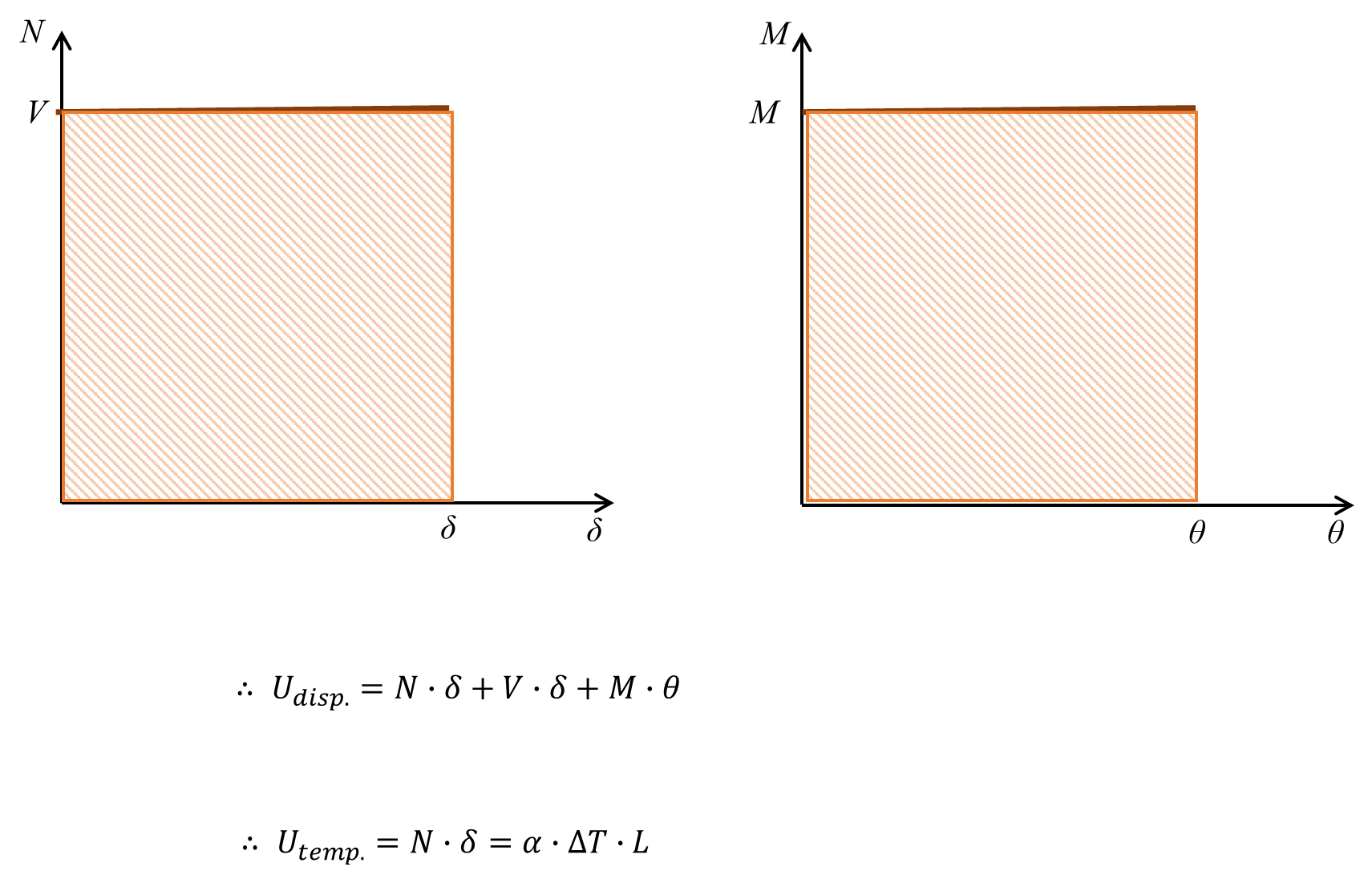
- Us : Spring Energy
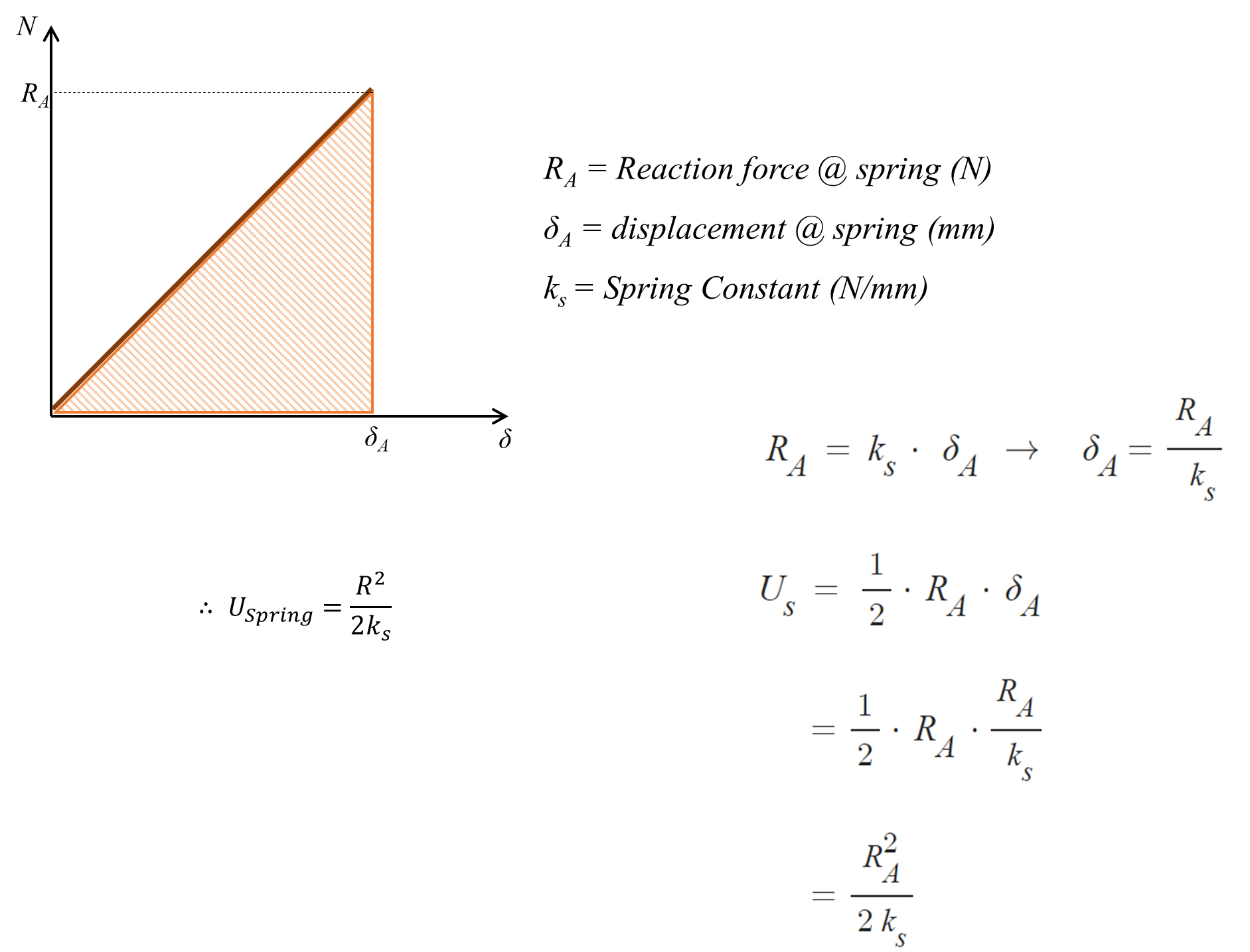
(6) 부정정력 산정 (카스틸리아노 제2정리)
- 변위가 0이 되는 경계조건을 해야함.
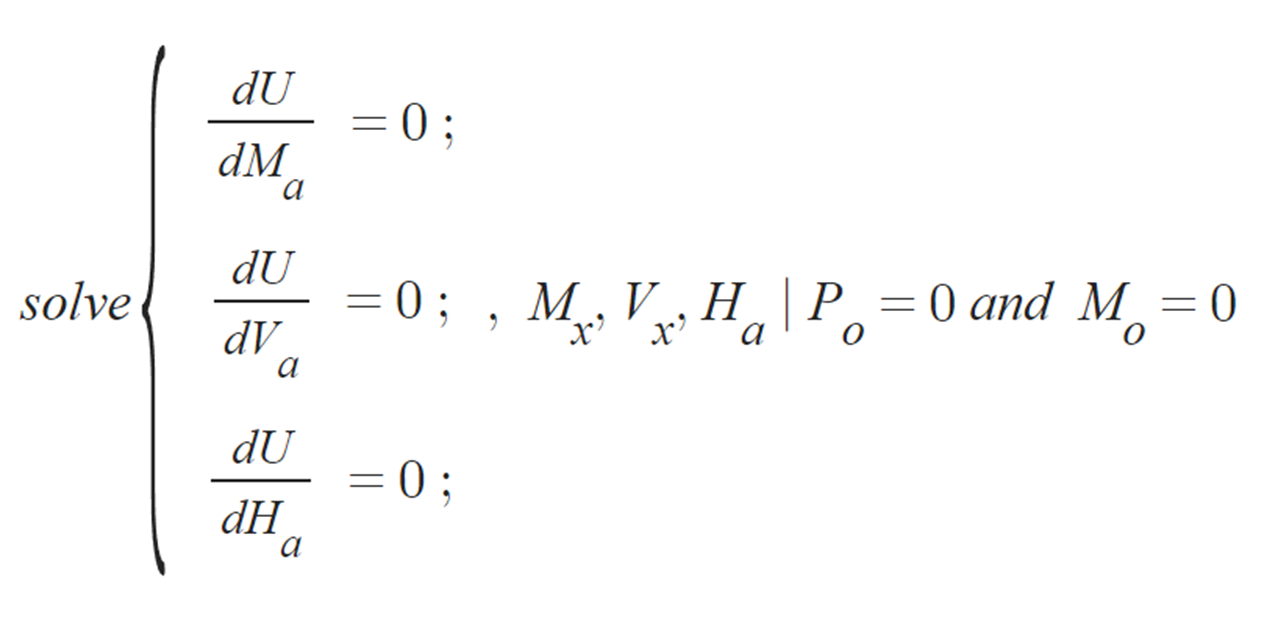
표시를 편미분으로 해야합니다. d 는 전미분의 표시입니다. 쨔샤
(7) 부재력 산정
부재력식에 부정정력 값 대입
N1 = 식 | Mx=값 and Vx= 값 and Hx = 값
.
.
.
M1 = 식 | Ma=값 and Va= 값 and Ha = 값
.
.
.
(8) 원하는 위치에서의 변위 산정
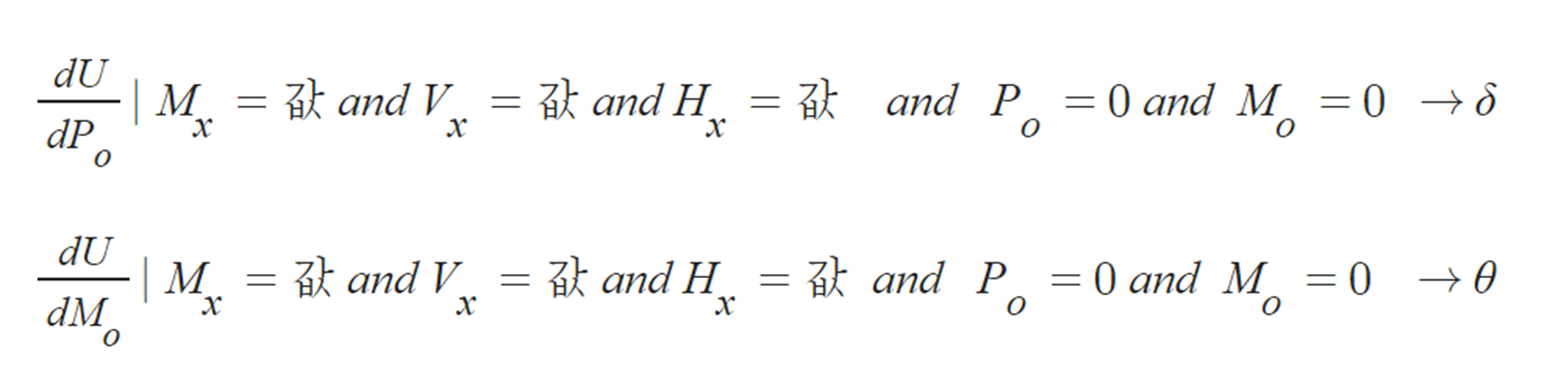
3) 예제문제
(1) 트러스 예시
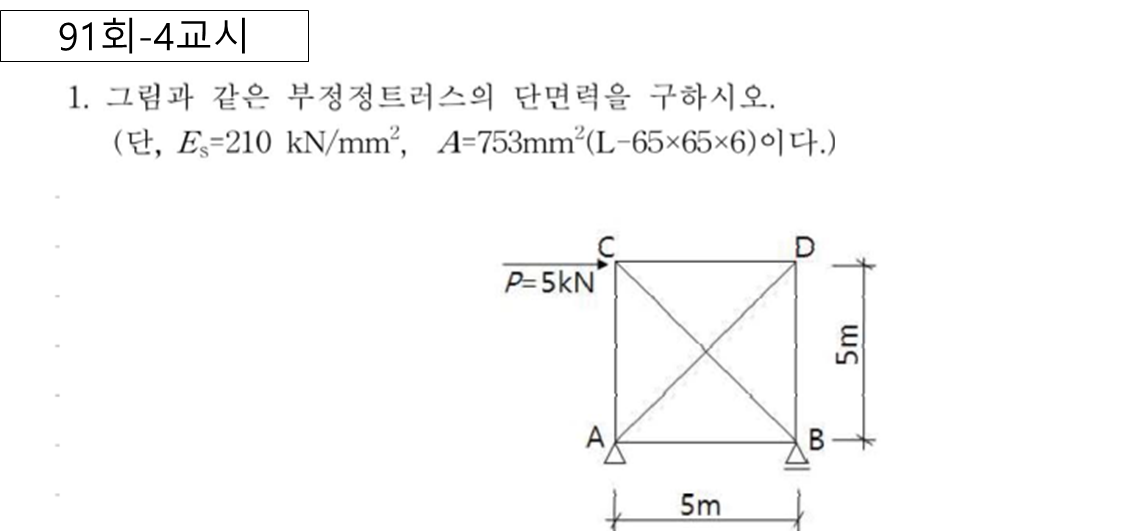
1차부정정 : 하나의 부재력 Q를 부정적력으로 간주하고 풀이
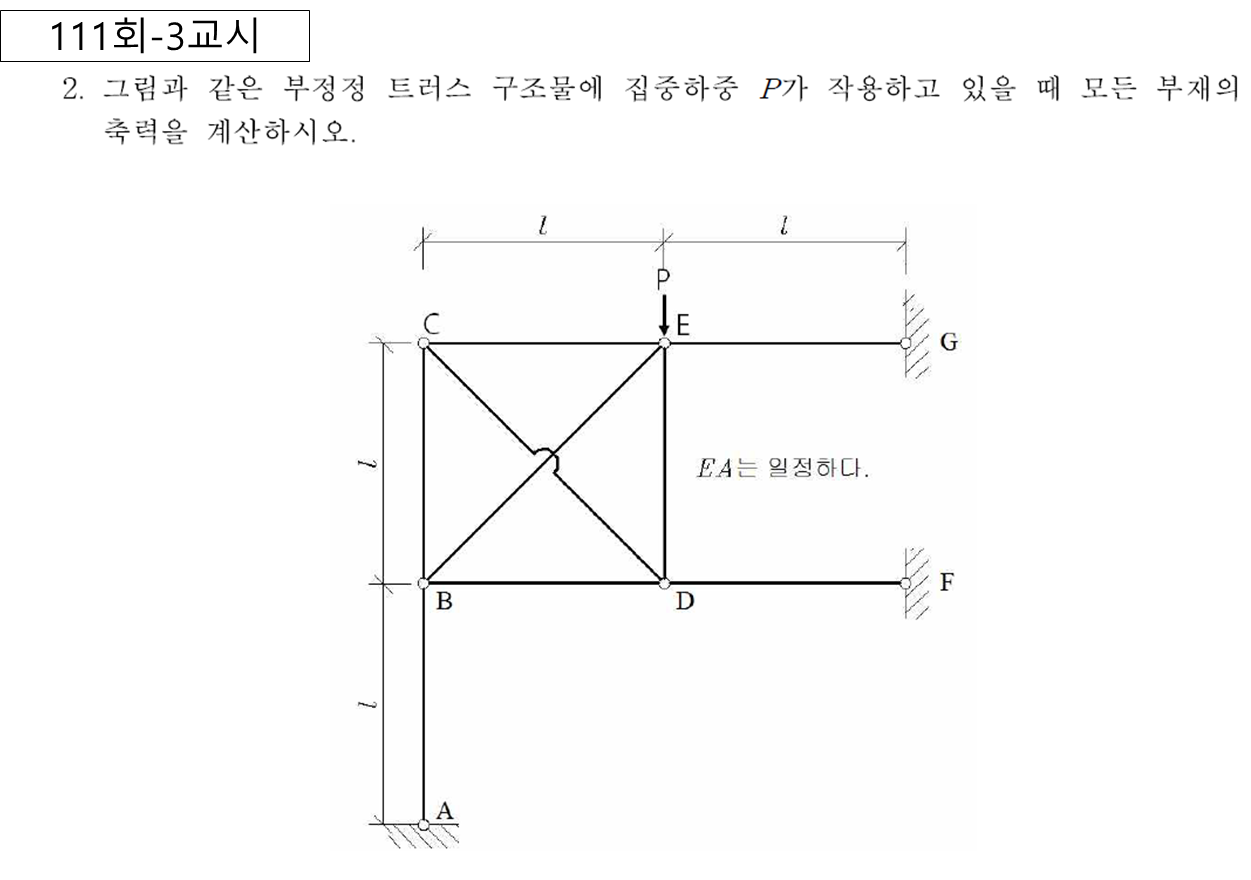
1차부정정 : 하나의 반력 R 를 부정적력으로 간주하고 풀이
(2) 보 예시
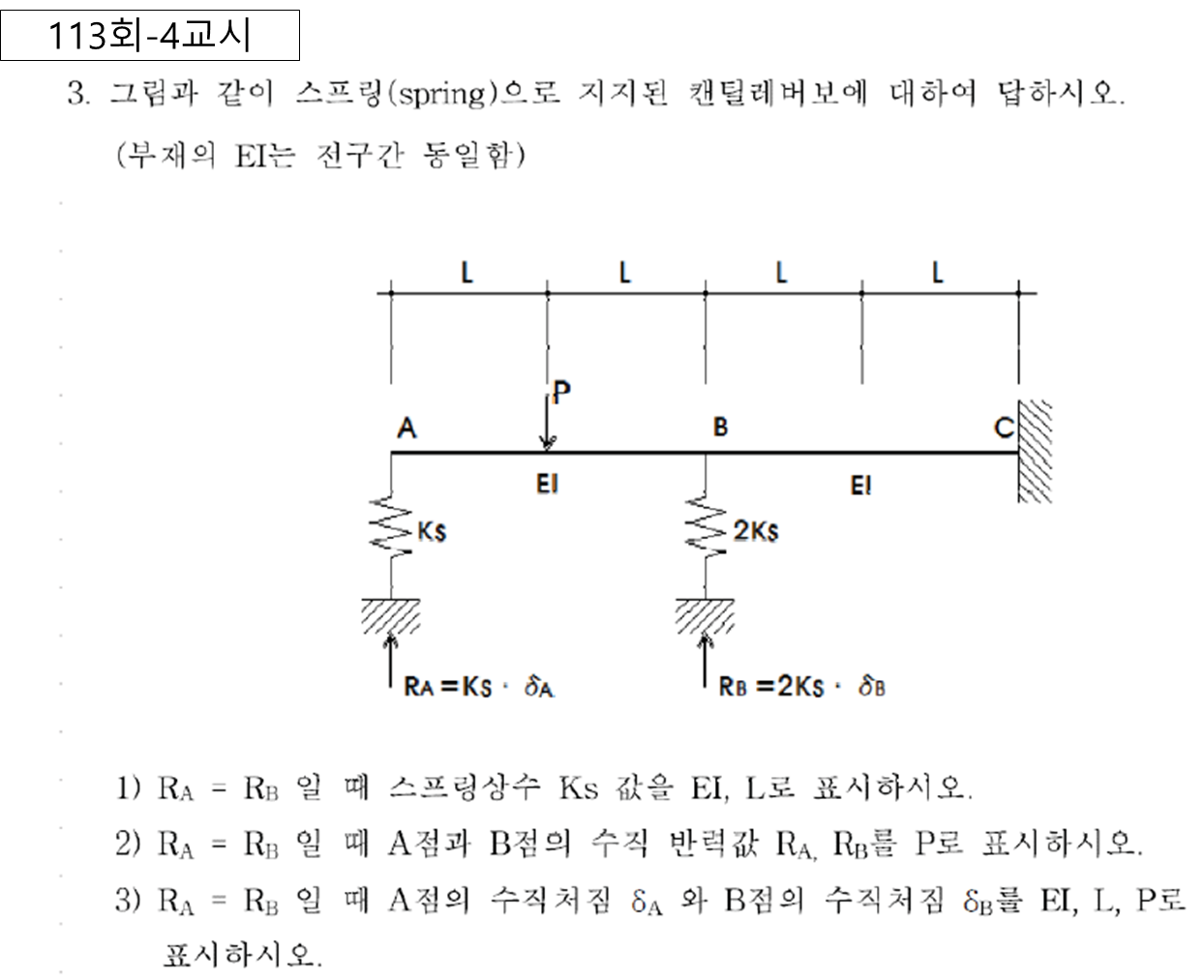
2차부정정 : 반력 RA, RB 를 부정적력으로 간주하고 풀이
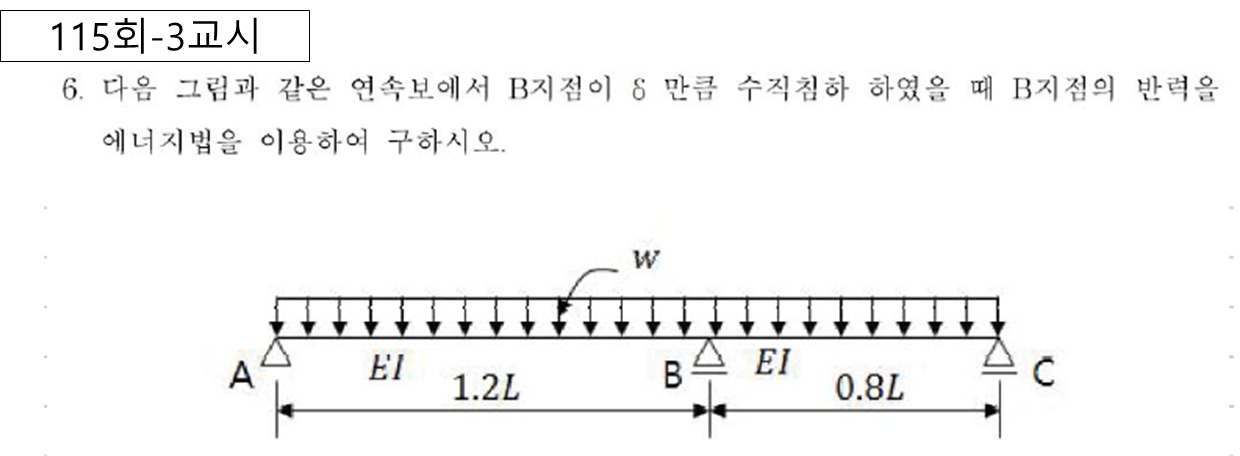
1차부정정 : 반력 VB 를 부정적력으로 간주하고 풀이
(3) 라멘 예시
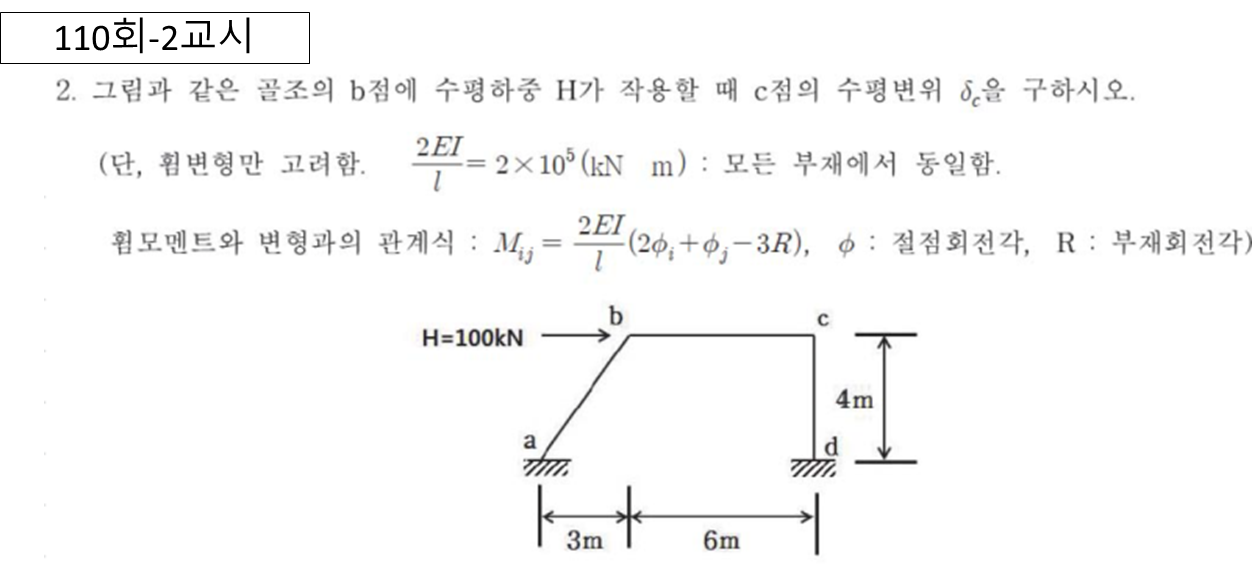
3차부정정 : 세개의 반력 V, H, M 를 부정적력으로 간주하고 풀이
(4) 복합 예시
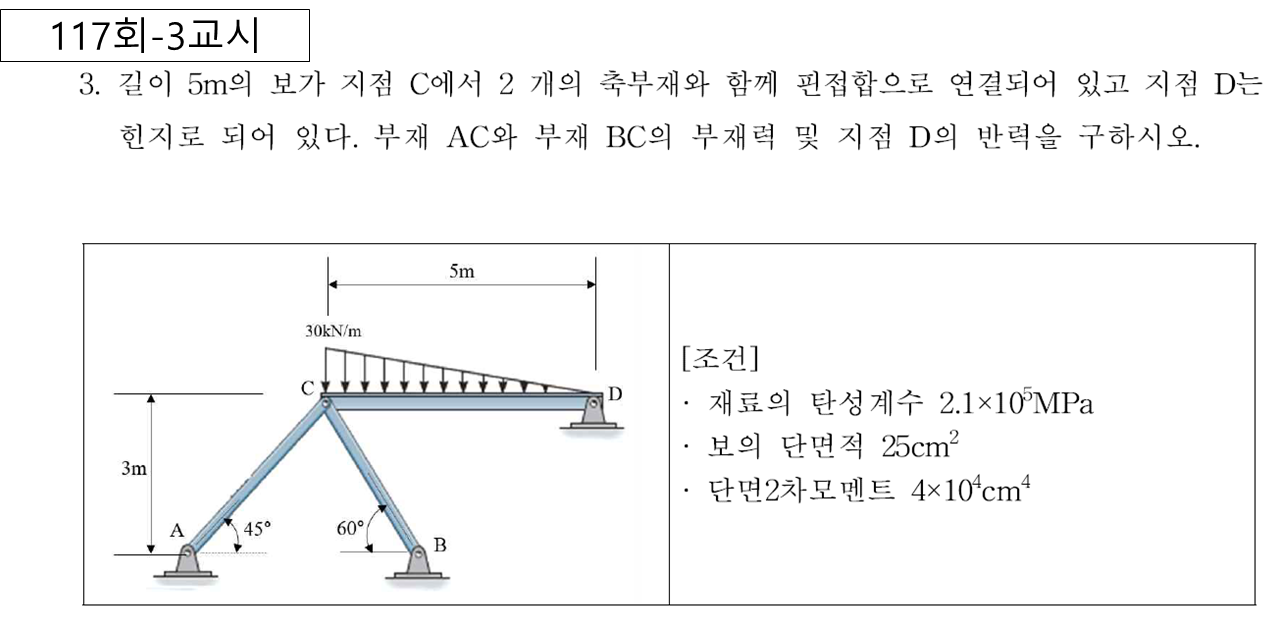
2차부정정 : 세개의 반력 Vc, Hc 를 부정적력으로 간주하고 풀이
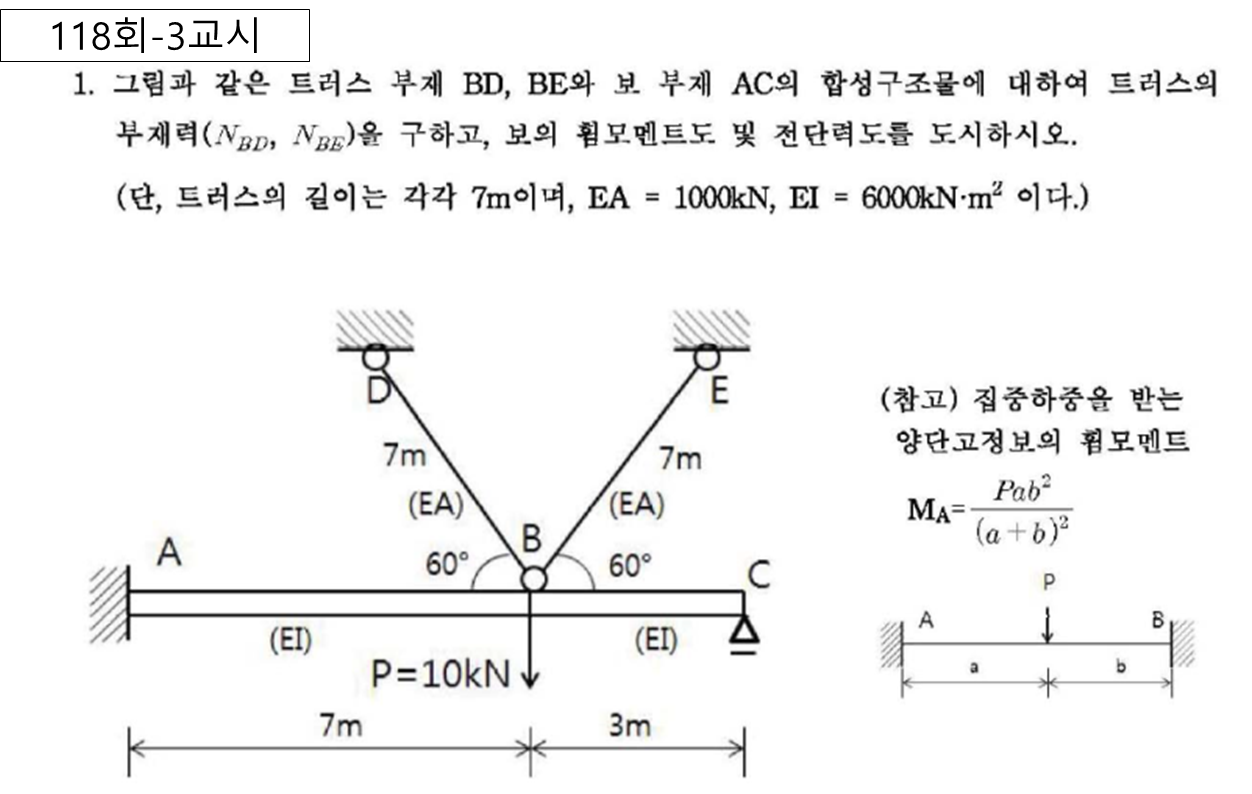
3차부정정 : 2개의 부정정력으로 풀이 가능 , VC 및 VB를 부정적력으로 간주하고 풀이
'역학 > [2] 구조역학' 카테고리의 다른 글
| [3] 구조역학 1. 부호의 규정 및 정정과 부정정 (0) | 2023.03.07 |
|---|---|
| [3] 구조역학 7. 부정정 구조물의 해석(모멘트분배법) (0) | 2023.01.08 |
| [3] 구조역학 5. 부정정 구조물의 해석 (처짐각법) (0) | 2022.12.04 |
| [3] 구조역학 6. 부정정 구조물의 해석(매트릭스변위법) (0) | 2022.09.03 |
| [3] 구조역학 3. 정정 구조물의 탄성 변형 (처짐 및 처짐각 산정) (0) | 2022.05.11 |



